题目内容
已知集合A={1,2,3,…,n}(n≥4),从集合A中取出4个不同的数构成有序数组(a1,a2,a3,a4),若对任意的2≤i≤4,都存在1≤j<i,使得|ai-aj|=1,则称该数组为“1-数组”,则“1-数组”共有 个.
考点:元素与集合关系的判断
专题:集合
分析:由“1-数组”的定义可得a1,a2,a3,a4,为连续的四个正整数,分析出从n个正整数中抽取4个连续的整数有n-3种方法,这四个整数排列满足定义又有8种不同情况,进而由分步乘法原理得到答案.
解答:
解:由“1-数组”的定义可得a1,a2,a3,a4,为连续的四个正整数,
不妨令取出的4个满足条件的数依次为:1,2,3,4,
则满足条件的排列有:
(1,2,3,4),(2,1,3,4),(2,3,1,4),(2,3,4,1),
(3,2,1,4),(3,2,4,1),(3,4,2,1),(4,3,2,1)共8种,
∵从n个正整数中抽取4个连续的整数有n-3种方法,
故“1-数组”共有8×(n-3)=8n-24种
故答案为:8n-24
不妨令取出的4个满足条件的数依次为:1,2,3,4,
则满足条件的排列有:
(1,2,3,4),(2,1,3,4),(2,3,1,4),(2,3,4,1),
(3,2,1,4),(3,2,4,1),(3,4,2,1),(4,3,2,1)共8种,
∵从n个正整数中抽取4个连续的整数有n-3种方法,
故“1-数组”共有8×(n-3)=8n-24种
故答案为:8n-24
点评:本题考查的知识点是元素与集合关系的判断,综合和排列组合,分类分步原理,难度较大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在△ABC中,已知sin2A+sin2B+sin2C=2,则△ABC为( )
| A、等腰三角形 |
| B、等边三角形 |
| C、直角三角形 |
| D、等腰直角三角形 |
已知数列{an},则“an+1>an-1”是“数列{an}为递增数列”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
 如图,在△ABC中,已知A(5,-2)、B(7,3),且AC边的中点M在y轴上,BC的中点N在x轴上,求这个三角形三边所在直线的方程.
如图,在△ABC中,已知A(5,-2)、B(7,3),且AC边的中点M在y轴上,BC的中点N在x轴上,求这个三角形三边所在直线的方程.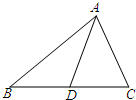 如图,已知△ABC中,∠BAD=30°,∠CAD=45°,AB=3,AC=2,则
如图,已知△ABC中,∠BAD=30°,∠CAD=45°,AB=3,AC=2,则