题目内容
14.已知函数$f(x)=\frac{1}{3}{x^3}-\frac{1}{2}{x^2}-2x+1$,(1)求函数f(x)的极值;
(2)若对?x∈[-2,3],都有s≥f(x)恒成立,求出s的范围.
分析 (1)利用导数求函数的极值即可;
(2)由题意可得只要s≥f(x)max即可,利用导数求得函数f(x)的最大值即可;
解答 解:(1)f′(x)=x2-x-2=(x-2)(x+1)=0,解得x=2或x=-1,
| x | (-∞,-1) | -1 | (-1,2) | 2 | (2,+∞) |
| f′(x) | + | 0 | - | 0 | + |
f(x) | 递增 | $\frac{13}{6}$ | 递减 | -$\frac{7}{3}$ | 递增 |
(2)f(-2)=$\frac{1}{3}$,f(3)=-$\frac{1}{2}$,
因此在区间[-2,3]的最大值是$\frac{13}{6}$,最小值是-$\frac{7}{3}$,
∴s≥$\frac{13}{6}$.
点评 本题只要考查利用导数研究函数的极值及最值等知识,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.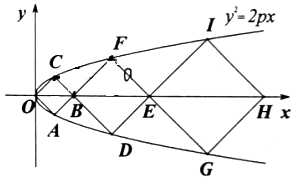 如图所示,O是坐标原点,三个正方形OABC、BDEF、EGHI的顶点中,O、A、C、D、F、G、I七个点都在抛物线y2=2px(p>0)上,另外,B、E、H三个点都在x轴上,则这三个正方形的面积之比( )
如图所示,O是坐标原点,三个正方形OABC、BDEF、EGHI的顶点中,O、A、C、D、F、G、I七个点都在抛物线y2=2px(p>0)上,另外,B、E、H三个点都在x轴上,则这三个正方形的面积之比( )
 如图所示,O是坐标原点,三个正方形OABC、BDEF、EGHI的顶点中,O、A、C、D、F、G、I七个点都在抛物线y2=2px(p>0)上,另外,B、E、H三个点都在x轴上,则这三个正方形的面积之比( )
如图所示,O是坐标原点,三个正方形OABC、BDEF、EGHI的顶点中,O、A、C、D、F、G、I七个点都在抛物线y2=2px(p>0)上,另外,B、E、H三个点都在x轴上,则这三个正方形的面积之比( )| A. | 1:2:3 | B. | 1:4:9 | C. | 2:3:4 | D. | 4:9:16 |
2.定义在R上的偶函数f(x)满足f(2-x)=f(x),且在[-3,-2]上是减函数,α,β是锐角三角形的两个内角,下列不等式正确的是( )
| A. | f(sinα)>f(cosβ) | B. | f(sinα)<f(cosβ) | C. | f(cosα)<f(cosβ) | D. | f(sinα)>f(sinβ) |
9.已知命题p:?x∈R,mx2+1<0,命题q:?x∈R,x2+mx+1>0,若p∧q为真命题,则实数m的取值范围是( )
| A. | (-∞,-2) | B. | [-2,0) | C. | (-2,0) | D. | (0,2) |
19.如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的体积为( )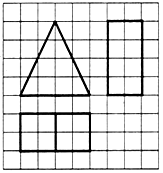

| A. | 16 | B. | $\frac{16}{3}$ | C. | 32 | D. | 48 |
3.在三角形ABC中,已知A=60°,b=1,其面积为$\sqrt{3}$,则$\frac{a+b+c}{sinA+sinB+sinc}$为( )
| A. | $3\sqrt{3}$ | B. | $\frac{{\sqrt{39}}}{2}$ | C. | $\frac{{26\sqrt{3}}}{3}$ | D. | $\frac{{2\sqrt{39}}}{3}$ |
4.已知函数f(x)=(x2+ax+b)(ex-e),a,b∈R,当x>0时,f(x)≥0,则实数a的取值范围为( )
| A. | -2≤a≤0 | B. | -1≤a≤0 | C. | a≥-1 | D. | 0≤a≤1 |