题目内容

8．用与球心距离为2的平面去截球，所得的截面面积为π，则球的表面积为（　　）
A．$\frac{20π}{3}$B．20πC．12πD．100π

分析 求出小圆的半径，然后利用球心到该截面的距离为2m，小圆的半径，通过勾股定理求出球的半径，即可求出球的表面积．

解答 解：用一平面去截球所得截面的面积为π，所以小圆的半径为：1；
已知球心到该截面的距离为2，所以球的半径为：$\sqrt{1+4}$=$\sqrt{5}$
所以表面积为4π•5=20π．
故选：B．

点评 本题是基础题，考查球的小圆的半径，球心到该截面的距离，球的半径之间的关系，满足勾股定理，考查计算能力．

练习册系列答案
相关题目
16．函数y=log0.4（-x2+3x+4）的值域是（-2，+∞）．
17．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右焦点分别为F1（-1，0）、F2（1，0），P为双曲线上任一点，若双曲线的离心率的取值范围为[$\sqrt{2}$，2]，则$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$最小值的取值范围是（　　）
A．[$\frac{1}{2}$，$\frac{3}{4}$]B．[-$\frac{3}{4}$，-$\frac{1}{2}$]C．[-$\frac{1}{2}$，-$\frac{1}{4}$]D．[$\frac{1}{4}$，$\frac{1}{2}$]
14．计算：（-1006）0+（$\frac{16}{81}$）${\;}^{-\frac{1}{4}}$+（3$\frac{3}{8}$）${\;}^{\frac{1}{3}}$．
3．在△ABC中，∠BAC=120°，AB=2，AC=1，D是边BC上的点，且|BD|=2|DC|，则$\overrightarrow{AD}$•$\overrightarrow{BC}$的值为（　　）
A．0B．1C．$\frac{1}{3}$D．-$\frac{1}{3}$
13．已知向量$\overrightarrow{a}$，$\overrightarrow{b}$满足|$\overrightarrow{a}$|=2|$\overrightarrow{b}$|≠0，且关于x的函数f（x）=2x3-3|$\overrightarrow{a}$|x2+6$\overrightarrow{a}$•$\overrightarrow{b}$x+5在实数集R上有极值，则向量$\overrightarrow{a}$，$\overrightarrow{b}$的夹角的取值范围是（　　）
A．（$\frac{π}{3}$，π）B．（$\frac{π}{3}$，π]C．[$\frac{π}{3}$，π]D．（0，$\frac{π}{3}$）
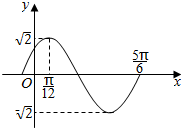20．函数f（x）=Asin（ωx+ϕ）$（A＞0，ω＞0，|φ|＜\frac{π}{2}）$的部分图象如图所示．
（1）分别求出A，ω，ϕ并确定函数f（x）的解析式；
（2）求出f（x）的单调递增区间；
（3）求不等式-$\sqrt{2}$≤f（x）≤1的解集．
17．已知正项数列{an}的前n项和为sn，且a1=2，anan+1=2（Sn+1）．
（1）求数列{an}的通项公式；
（2）若数列{bn}满足${b_1}=-\frac{{\sqrt{2}}}{2}$，${b_n}=\frac{1}{{{a_n}\sqrt{{a_{n-1}}}+{a_{n-1}}\sqrt{a_n}}}（n≥2，且n∈{N^*}）$，求{bn}的前n项和Tn
（3）数列{cn}满足lgc1=$\frac{1}{3}$，lgcn=$\frac{{{a_{n-1}}}}{3^n}$（n≥2，且n∈N*），试问是否存在正整数p，q其中（1＜p＜q），使c1，cp，cq成等比数列？若存在求出满足条件所有的数组（p，q）；若不存在请说明理由．
18．设函数f（x）=$\frac{{e}^{2}-1}{x}$，x≠0．其中e=2.71828…
（1）设h（x）=f（x）+$\frac{1}{x}$，求函数h（x）在[$\frac{1}{2}$，2]上的值域；
（2）证明：对任意正数a，存在正数x，使不等式|f（x）-1|＜a成立．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网