题目内容
15. 株洲市某中学利用周末组织教职员工进行了一次秋季登石峰山健身的活动,有N人参加,现将所有参加人员按年龄情况分为[20,25),[25,30),[30,35],[35,40),[40,45),[45,50),[50,55)等七组,其频率分布直方图如图所示.已知[35,40)之间的参加者有8人.
株洲市某中学利用周末组织教职员工进行了一次秋季登石峰山健身的活动,有N人参加,现将所有参加人员按年龄情况分为[20,25),[25,30),[30,35],[35,40),[40,45),[45,50),[50,55)等七组,其频率分布直方图如图所示.已知[35,40)之间的参加者有8人.(1)求N和[30,35]之间的参加者人数N1;
(2)已知[30,35)和[35,40)之间各有2名数学教师,现从这两个组中各选取2人担任接待工作,设两组的选择互不影响,求两组选出的人中都至少有1名数学教师的概率?
(3)组织者从[45,50)之间的参加者(其中共有4名女教师,其余全为男教师)中随机选取3名担任后勤保障工作,其中女教师的人数为ξ,求ξ的分布列和均值.
分析 (1)先求出年龄在[35,40)之间的概率,由此能求出总人数和年龄在[30,35)之间的志愿者人数.
(2)先求出从年龄在[30,35)之间选出的人中至少有2名数学教师的概率,再求出从年龄在[35,40)之间选出的人中至少有1名数学教师的概率,由此能求出两组选出的人中都至少有1名数学教师的概率.
(3)ξ的可能取值为1,2,3,分别求出相应的概率,由此能求出ξ的分布列和均值.
解答 解:(1)年龄在[35,40)之间的概率为0.04×5=0.2,
所以总人数$N=\frac{8}{0.2}=40$,
因为1-(0.01+0.03+0.04+0.03+0.02+0.01)×5=0.3
所以年龄在[30,35)之间的志愿者人数为40×0.3=12…4分
(2)记事件B=从年龄在[30,35)之间选出的人中至少有2名数学教师
因为年龄在[30,35)之间的人数为12,所以$P(B)=1-\frac{{{C_{10}}^2}}{{{C_{12}}^2}}=\frac{7}{22}$
记事件C=从年龄在[35,40)之间选出的人中至少有1名数学教师
因为年龄在[35,40)之间的人数为8,所以$P(C)=1-\frac{{{C_6}^2}}{{{C_8}^2}}=\frac{13}{28}$
则两组选出的人中都至少有1名数学教师的概率P(A)=$\frac{7}{22}•\frac{13}{28}$=$\frac{13}{88}$.
(3)年龄在[45,55)之间的人数为6人,其中女教师4人,ξ的可能取值为1,2,3
P($P(ξ=1)=\frac{{{C_4}^1{C_2}^2}}{{{C_6}^3}}=\frac{1}{5}$,
$P(ξ=2)=\frac{{{C_4}^2{C_2}^1}}{{{C_6}^3}}=\frac{3}{5}$,
$P(ξ=3)=\frac{{{C_4}^3}}{{{C_6}^3}}=\frac{1}{5}$,
所以ξ的分布列为
| ξ | 1 | 2 | 3 |
| p | $\frac{1}{5}$ | $\frac{3}{5}$ | $\frac{1}{5}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用.

| A. | 0 | B. | 1 | C. | $\frac{1}{3}$ | D. | -$\frac{1}{3}$ |
| A. | m<1 | B. | m≤1 | C. | m≥3 | D. | m>3 |
| A. | 2n | B. | 2n-1 | C. | 2n | D. | 2n-1 |
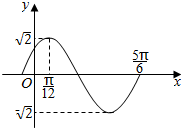 函数f(x)=Asin(ωx+ϕ)$(A>0,ω>0,|φ|<\frac{π}{2})$的部分图象如图所示.
函数f(x)=Asin(ωx+ϕ)$(A>0,ω>0,|φ|<\frac{π}{2})$的部分图象如图所示.