题目内容
13.在等差数列{an}中,a2=5,a1+a3+a4=19.(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{bn}前n项和为Sn,且Sn+$\frac{{a}_{n}-1}{{2}^{n}}$=λ(λ为常数),令cn=bn+1(n∈N*).求数列{cn}的前n项和Tn.
分析 (Ⅰ)设等差数列{an}的公差为d,运用等差数列的通项公式,列方程解方程可得首项和公差,即可得到所求通项公式;
(Ⅱ)求得Sn=λ-n•($\frac{1}{2}$)n-1,当n≥2时,bn=Sn-Sn-1,求得cn=bn+1=(n-1)•($\frac{1}{2}$)n,再由数列的求和方法:错位相减法,结合等比数列的求和公式,化简整理可得所求和.
解答 解:(Ⅰ)等差数列{an}中,a2=5,a1+a3+a4=19,
设等差数列{an}的公差为d,
可得a1+d=5,3a1+5d=19,
解得a1=3,d=2,
则an=a1+(n-1)d=3+2(n-1)=2n+1;
(Ⅱ)Sn+$\frac{{a}_{n}-1}{{2}^{n}}$=λ(λ为常数),
可得Sn+$\frac{2n}{{2}^{n}}$=λ,
即有Sn=λ-n•($\frac{1}{2}$)n-1,
当n≥2时,bn=Sn-Sn-1=λ-n•($\frac{1}{2}$)n-1-λ+(n-1)•($\frac{1}{2}$)n-2=(n-2)•($\frac{1}{2}$)n-1,
cn=bn+1=(n-1)•($\frac{1}{2}$)n,
数列{cn}的前n项和Tn=0•($\frac{1}{2}$)+1•($\frac{1}{2}$)2+2•($\frac{1}{2}$)3+…+(n-1)•($\frac{1}{2}$)n,
$\frac{1}{2}$Tn=0•($\frac{1}{2}$)2+1•($\frac{1}{2}$)3+2•($\frac{1}{2}$)4+…+(n-1)•($\frac{1}{2}$)n+1,
两式相减可得,$\frac{1}{2}$Tn=0+($\frac{1}{2}$)2+($\frac{1}{2}$)3+($\frac{1}{2}$)4+…+($\frac{1}{2}$)n-(n-1)•($\frac{1}{2}$)n+1
=$\frac{\frac{1}{4}(1-\frac{1}{{2}^{n-1}})}{1-\frac{1}{2}}$-(n-1)•($\frac{1}{2}$)n+1,
可得数列{cn}的前n项和Tn=1-(n+1)•($\frac{1}{2}$)n.
点评 本题考查等差数列的通项公式的求法,注意运用方程思想,考查数列的求和方法:错位相减法,考查化简整理的运算能力,属于中档题.

 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案| A. | [0,+∞) | B. | (0,+∞) | C. | (1,2) | D. | (1,+∞) |
| A. | g(π)<g(3)<g($\sqrt{2}$) | B. | g(π)<g($\sqrt{2}$)<g(3) | C. | g($\sqrt{2}$)<g(3)<g(π) | D. | g($\sqrt{2}$)<g(π)<g(3) |
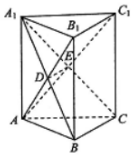 如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,A1B与AB1交于点D,A1C与AC1交于点E.
如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,A1B与AB1交于点D,A1C与AC1交于点E.