题目内容
若p是q的必要条件，s是q的充分条件，那么下列推理一定正确的是（ ）
| A、￢p?￢s | B、p?s |
| C、￢p⇒￢s | D、￢s⇒￢p |
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：根据充分条件和必要条件的定义，以及逆否命题的等价性，即可得到结论．
解答：
解：∵p是q的必要条件，s是q的充分条件，
∴q⇒p，s⇒q，
∴s⇒p，
则根据逆否命题的等价性可知：￢p⇒￢s，
故选：C
∴q⇒p，s⇒q，
∴s⇒p，
则根据逆否命题的等价性可知：￢p⇒￢s，
故选：C
点评：本题主要考查充分条件和必要条件的应用，利用逆否命题的等价性是解决本题的关键，比较基础．
练习册系列答案
相关题目
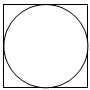一次实验：向如图所示的正方形中随机撒一大把豆子，经查数，落在正方形中的豆子的总数为N粒，其中m（m＜N）粒豆子落在该正方形的内切圆内，以此估计圆周率π为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
已知cos(α-
)+sinα=
，且α∈(0，
)则sin(α+
π)的是（ ）
| π |
| 6 |
| 4 |
| 5 |
| 3 |
| π |
| 3 |
| 5 |
| 12 |
A、-
| ||||
B、
| ||||
C、
| ||||
D、
|
从甲、乙两个城市分别随机抽取6台自动售货机，对其销售额进行统计，统计数据用茎叶图表示（如图所示），设甲、乙两组数据的平均数分别为. |
| x |
. |
| x |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知函数f（x）=
．设a=log
，则f（f（a））的值等于（ ）
|
| 1 |
| 2 |
| 3 |
A、
| ||
| B、2 | ||
| C、3 | ||
| D、-2 |
下列等式中，成立的是（ ）
A、sin（
| ||||
| B、sin（x+2π）=sinx | ||||
| C、sin（2π+x）=-sinx | ||||
| D、cos（π+x）=cosx |
若sinα+cosα=
(0＜α＜π)，则tanα=（ ）
| 7 |
| 13 |
A、-
| ||
B、
| ||
C、-
| ||
D、
|