题目内容
6.集合A={x|-3<x<7},B={x|t+1<x<2t-1},若B⊆A,则实数t的取值范围是(-∞,4].分析 由B⊆A,根据B=∅和B≠∅两种情况分类讨论,能求出实数t的取值范围.
解答 解:∵集合A={x|-3<x<7},B={x|t+1<x<2t-1},B⊆A,
∴当B=∅时,t+1≥2t-1,解得t≤2.
当B≠∅时,$\left\{\begin{array}{l}{t+1<2t-1}\\{t+1≥-3}\\{2t-1≤7}\end{array}\right.$,解得2<t≤4.
综上,t≤4.
∴实数t的取值范围是(-∞,4].
故答案为(-∞,4].
点评 本题考查实数的取值范围的求法,是基础题,解题时要认真审题,注意子集性质的合理运用.

练习册系列答案
相关题目
14.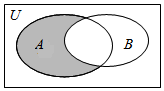 设全集U=R,A={x|x(x-2)<0},B={x|y=$\sqrt{1-x}$},则图中阴影部分表示的集合为( )
设全集U=R,A={x|x(x-2)<0},B={x|y=$\sqrt{1-x}$},则图中阴影部分表示的集合为( )
 设全集U=R,A={x|x(x-2)<0},B={x|y=$\sqrt{1-x}$},则图中阴影部分表示的集合为( )
设全集U=R,A={x|x(x-2)<0},B={x|y=$\sqrt{1-x}$},则图中阴影部分表示的集合为( )| A. | {x|0<x≤1} | B. | {x|1<x<2} | C. | {x|x≤1} | D. | {x|1≤x<2} |
18.在△ABC中,已知a=7,b=5,c=3,则角A大小为( )
| A. | 120° | B. | 90° | C. | 60° | D. | 45° |
 如图,有一块半径为2的半圆形空地,计划绿化成等腰梯形ABCD形状的草坪,它的下底AB是⊙O的直径,上底CD的端点在圆周上,设草坪ABCD的周长为y.
如图,有一块半径为2的半圆形空地,计划绿化成等腰梯形ABCD形状的草坪,它的下底AB是⊙O的直径,上底CD的端点在圆周上,设草坪ABCD的周长为y.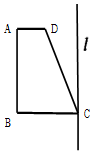 如图,梯形ABCD中,AD∥BC,∠ABC=90°,AD=1,BC=2,∠DCB=60°,在平面ABCD内过点C作l⊥CB,将梯形ABCD以l为轴旋转一周
如图,梯形ABCD中,AD∥BC,∠ABC=90°,AD=1,BC=2,∠DCB=60°,在平面ABCD内过点C作l⊥CB,将梯形ABCD以l为轴旋转一周