题目内容

18．在△ABC中，已知a=7，b=5，c=3，则角A大小为（　　）
A．120°B．90°C．60°D．45°

分析 由已知利用余弦定理可求cosA的值，结合A的范围即可得解A的值．

解答 解：∵a=7，b=5，c=3，
∴由余弦定理可得：cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{25+9-49}{2×5×3}$=-$\frac{1}{2}$，
又∵A∈（0°，180°），
∴A=120°．
故选：A．

点评 本题主要考查了余弦定理在解三角形中的应用，考查了转化思想，属于基础题．

练习册系列答案
相关题目
8．已知函数f（x）=ax2-2lnx．
（Ⅰ）若f（x）在x=e处取得极值，求a的值；
（Ⅱ）若x∈（0，e]，求f（x）的单调区间；
（Ⅲ） 设a＞$\frac{1}{{e}^{2}}$，g（x）=-5+ln$\frac{x}{a}$，?x1，x2∈（0，e]，使得|f（x1）-g（x2）|＜9成立，求a的取值范围．
9．设f（x）是偶函数，且在（0，+∞）上是增函数，又f（5）=0，则使f（x）＞0的x的取值范围是（　　）
A．-5＜x＜0或x＞5B．x＜-5或x＞5C．-5＜x＜5D．x＜-5或0＜x＜5
6．集合A={x|-3＜x＜7}，B={x|t+1＜x＜2t-1}，若B⊆A，则实数t的取值范围是（-∞，4]．
13．市场上有一种新型的强力洗衣粉，特点是去污速度快，已知每投放a（1≤a≤4且a∈R）个单位的洗衣粉液在一定量水的洗衣机中，它在水中释放的浓度y（克/升）随着时间x（分钟）变化的函数关系式近似为y=af（x），其中f（x）=$\left\{\begin{array}{l}\frac{16}{8-x}-1，0≤x≤4\\ 5-\frac{1}{2}x，4＜x≤10\end{array}$，若多次投放，则某一时刻水中的洗衣液浓度为每次投放的洗衣液在相应时刻所释放的浓度之和，根据经验，当水中洗衣液的浓度不低于4（克/升）时，它才能起有效去污的作用．
（1）若只投放一次4个单位的洗衣液，则有效去污时间可能达几分钟？
（2）若先投放2个单位的洗衣液，6分钟后投放a个单位的洗衣液，要使接下来的4分钟中能够持续有效去污，试求a的最小值（精确到0.1，参考数据：$\sqrt{2}$取1.4）
3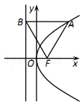．如图，抛物线的顶点在坐标原点，焦点为F，过抛物线上一点A（3，y）作准线l作垂线，垂直为B，若|AB|=|BF|，则抛物线的标准方程是（　　）
A．y2=$\frac{1}{2}$xB．y2=xC．y2=2xD．y2=4x
10．已知函数f（x）=$\overrightarrow m•\overrightarrow n$，其中$\overrightarrow m=（sinωx+cosωx，\sqrt{3}cosωx）$，$\overrightarrow n=（cosωx-sinωx，2sinωx）$，其中ω＞0，若f（x）相邻两对称轴间的距离为$\frac{π}{2}$．
（Ⅰ） 求函数f（x）的单调递增区间；
（Ⅱ）在△ABC中，a，b，c分别为角A、B、C的对边，a=$\sqrt{3}$，b+c=3，f（A）=1，求△ABC的面积．
7．图中的阴影表示的集合中是（　　）
A．A∩∁UBB．B∩∁UAC．∁U（A∩B）D．∁U（A∪B）
8．若函数f（x）=axsinx-$\frac{3}{2}（{a∈R}）$，且在区间$[{0，\frac{π}{2}}]$上的最大值为$\frac{π-3}{2}$，则实数a的值为1．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网