题目内容
3.已知A,B是椭圆3x2+y2=m(m>0)上不同两点,线段AB的中点为N(1,3).则m的取值范围为(12,+∞),AB所在的直线方程为y=-x+4.分析 由题意可得N在椭圆内,代入椭圆方程解不等式可得m的范围;设A(x1,y1),B(x2,y2),代入椭圆方程,运用点差法和中点坐标公式,以及斜率公式,结合直线的点斜式方程,可得直线AB的方程.
解答 解:由题意可得N(1,3)在椭圆内,
可得3+32<m,即有m>12;
设A(x1,y1),B(x2,y2),
可得3x12+y12=m,
3x22+y22=m,
相减可得,3(x1-x2)(x1+x2)+(y1-y2)(y1+y2)=0,
即有AB的斜率为k=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=-$\frac{{3(x}_{1}+{x}_{2})}{{y}_{1}+{y}_{2}}$=-$\frac{3×2}{6}$=-1,
即有直线AB的方程为y-3=-(x-1),即为y=-x+4.
故答案为:(12,+∞),y=-x+4.
点评 本题考查椭圆的方程的运用,考查点差法的运用,以及直线的斜率公式和中点坐标公式,考查运算能力,属于中档题.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
20.程序框图如图所示:如果输入x=5,则输出结果为( )


| A. | 325 | B. | 109 | C. | 973 | D. | 295 |
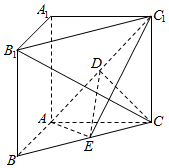 如图,在直三棱柱ABC-A1B1C1中,CC1⊥平面ABC,∠BAC=90°,AB=AC=AA1=2,且E是BC的中点,D是AC1中点.
如图,在直三棱柱ABC-A1B1C1中,CC1⊥平面ABC,∠BAC=90°,AB=AC=AA1=2,且E是BC的中点,D是AC1中点.