题目内容
18.已知正数x,y满足x+y=1,则$\frac{1}{x}$$+\frac{x}{y}$的最小值为3.分析 正数x,y满足x+y=1,把1代入$\frac{1}{x}$$+\frac{x}{y}$=$\frac{x+y}{x}$+$\frac{x}{y}$,化简利用基本不等式的性质即可得出.
解答 解:∵正数x,y满足x+y=1,
∴$\frac{1}{x}$$+\frac{x}{y}$=$\frac{x+y}{x}$+$\frac{x}{y}$=1+$\frac{y}{x}+\frac{x}{y}$≥$1+2\sqrt{\frac{y}{x}×\frac{x}{y}}$=3,当且仅当x=y=$\frac{1}{2}$时取等号.
∴$\frac{1}{x}$$+\frac{x}{y}$的最小值为3.
故答案为:3.
点评 本题考查了基本不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.某几何体的三视图如图所示,若该几何体的体积等于16+8π,则r等于( )
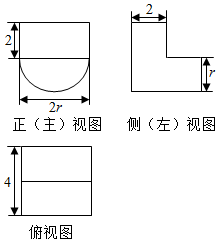

| A. | 1 | B. | 2 | C. | 2$\sqrt{2}$ | D. | 4 |
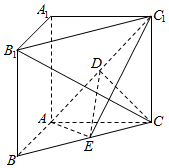 如图,在直三棱柱ABC-A1B1C1中,CC1⊥平面ABC,∠BAC=90°,AB=AC=AA1=2,且E是BC的中点,D是AC1中点.
如图,在直三棱柱ABC-A1B1C1中,CC1⊥平面ABC,∠BAC=90°,AB=AC=AA1=2,且E是BC的中点,D是AC1中点.