��Ŀ����
1����֪������R�ϵ�������f��x��=$\frac{{��}^{x}-{��}^{-x}}{2}$��g��x��=$\frac{{��}^{x}+{��}^{-x}}{2}$�����Ц�ΪԲ���ʣ���=3.1415926���������������⣺��f��x�����溯����g��x����ż������
��f��x����R�ϵ���������g��x����R�ϵļ�������
��f��x�������ֵ����Сֵ��g��x������Сֵ�������ֵ��
�ܶ�����x��R������f��2x��=2f��x��g��x����
��f��x������㣬g��x������㣮
������ȷ�������Т٢ۢܢݣ���������ȷ�������Ŷ����ϣ�
���� �����f��x��+f��-x��=0��g��x��-g��-x��=0���ʢ���ȷ��
��֪g��x��R�ϲ������Ǽ��������ʢڲ���ȷ��
���ж�f��x����R�ϵ���������g��x������������Ӷ��жϣ�
����f��2x��=$\frac{{��}^{2x}-{��}^{-2x}}{2}$��2f��x��g��x��=2•$\frac{{��}^{x}-{��}^{-x}}{2}$•$\frac{{��}^{-x}+{��}^{x}}{2}$=$\frac{{��}^{2x}-{��}^{-2x}}{2}$���ʢܳ�����
��֪f��0��=0��g��x����g��0��=1���ʢ���ȷ��
��� �⣺��f��x��+f��-x��=$\frac{{��}^{x}-{��}^{-x}}{2}$+$\frac{{��}^{-x}-{��}^{x}}{2}$=0��
g��x��-g��-x��=$\frac{{��}^{x}+{��}^{-x}}{2}$-$\frac{{��}^{-x}+{��}^{x}}{2}$=0��
��f��x�����溯����g��x����ż�������ʢ���ȷ��
��g��x����ż������
��g��x��R�ϲ������Ǽ��������ʢڲ���ȷ��
���ж�f��x����R�ϵ���������g��x�����������
��f��x�������ֵ����Сֵ��g��x������Сֵ�������ֵ��
�ʢ���ȷ��
f��2x��=$\frac{{��}^{2x}-{��}^{-2x}}{2}$��
2f��x��g��x��=2•$\frac{{��}^{x}-{��}^{-x}}{2}$•$\frac{{��}^{-x}+{��}^{x}}{2}$=$\frac{{��}^{2x}-{��}^{-2x}}{2}$��
�ʢܳ�����
��f��0��=0����f��x������㣬
��g��x����g��0��=1����g��x��û����㣻
�ʢ���ȷ��
�ʴ�Ϊ���٢ۢܢݣ�
���� ���⿼���˺��������ʵ��ж���Ӧ�ã����ڻ����⣮

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д� ����f��x��=2sin����x+�գ����أ�0��0�ܦա�$\frac{��}{2}$���IJ���ͼ����ͼ��ʾ������A��B����֮��ľ���Ϊ5����ô����˵����ȷ���ǣ�������
����f��x��=2sin����x+�գ����أ�0��0�ܦա�$\frac{��}{2}$���IJ���ͼ����ͼ��ʾ������A��B����֮��ľ���Ϊ5����ô����˵����ȷ���ǣ�������| A�� | ����f��x������С������Ϊ8 | |
| B�� | f��3��=-$\frac{1}{2}$ | |
| C�� | x=-1�Ǻ���f��x����һ���Գ��� | |
| D�� | ����f��x������ƽ��һ����λ���Ⱥ����õĺ���Ϊż���� |
| A�� | a��b��c | B�� | b��c��a | C�� | b��a��c | D�� | c��b��a |
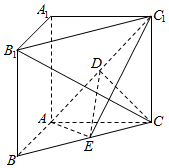 ��ͼ����ֱ������ABC-A1B1C1�У�CC1��ƽ��ABC����BAC=90�㣬AB=AC=AA1=2����E��BC���е㣬D��AC1�е㣮
��ͼ����ֱ������ABC-A1B1C1�У�CC1��ƽ��ABC����BAC=90�㣬AB=AC=AA1=2����E��BC���е㣬D��AC1�е㣮