题目内容
8.已知三棱柱ABC-A1B1C1的侧棱和底面垂直,底面是正三角形,侧棱长是底边长的2倍,若该三棱柱的各顶点都在球O的表面上,且球O的表面积为36π,则此三棱锥A-A1B1C1的体积为( )| A. | $\frac{121}{25}$ | B. | $\frac{81}{16}$ | C. | $\frac{16}{9}$ | D. | $\frac{9}{4}$ |
分析 通过球的内接体,说明几何体的中心是球的直径,由球的表面积求出球的半径,设出三棱柱的底面边长,通过解直角三角形求得a,然后由棱柱的体积公式得答案.
解答  解:如图,
解:如图,
∵三棱柱ABC-A1B1C1的所有棱长都相等,6个顶点都在球O的球面上,
∴三棱柱为正三棱柱,且其中心为球的球心,设为O,
再设球的半径为r,由球O的表面积为36π,得4πr2=36π,∴r=3.
设三棱柱的底面边长为a,则上底面所在圆的半径为$\frac{\sqrt{3}}{3}$a,且球心O到上底面中心H的距离OH=a,
∴32=a2+($\frac{\sqrt{3}}{3}$a)2,∴a=$\frac{3\sqrt{3}}{2}$.
则三棱柱的底面积为S=$\frac{\sqrt{3}}{4}×(\frac{3\sqrt{3}}{2})^{2}$=$\frac{27\sqrt{3}}{16}$.
∴三棱锥A-A1B1C1的体积为$\frac{1}{3}$×$\frac{27\sqrt{3}}{16}$×2×$\frac{3\sqrt{3}}{2}$=$\frac{81}{16}$.
故选:B.
点评 本题考查球的内接体与球的关系,球的半径的求解,考查计算能力,是中档题.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
19.函数f(x)=$\left\{\begin{array}{l}\frac{1}{2^x},x≤0\\ 2sin(2x+\frac{π}{6}),0<x<π\end{array}$若x1,x2,x3是方程f(x)+a=0三个不同的根,则x1+x2+x3的范围是( )
| A. | $(-1,\frac{π}{2})$ | B. | $(\frac{π}{3}-1,\frac{π}{3})$ | C. | $(\frac{π}{3}-1,\frac{π}{3}+1)$ | D. | $(\frac{π}{6},\frac{π}{6}+1)$ |
16.若a=log0.50.2,b=log20.2,c=20.2,则a,b,c的大小关系是( )
| A. | a<b<c | B. | b<c<a | C. | b<a<c | D. | c<b<a |
17.函数y=cos(πx+$\frac{π}{6}$)的一个单调增区间是( )
| A. | [-$\frac{2}{3}$,$\frac{1}{3}$] | B. | [$\frac{1}{3}$,$\frac{4}{3}$] | C. | [-$\frac{1}{6}$,$\frac{5}{6}$] | D. | [$\frac{5}{6}$,$\frac{11}{6}$] |
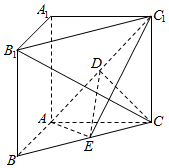 如图,在直三棱柱ABC-A1B1C1中,CC1⊥平面ABC,∠BAC=90°,AB=AC=AA1=2,且E是BC的中点,D是AC1中点.
如图,在直三棱柱ABC-A1B1C1中,CC1⊥平面ABC,∠BAC=90°,AB=AC=AA1=2,且E是BC的中点,D是AC1中点.