题目内容
2.当x>1时,lnx+$\frac{1}{x}$与1的大小关系为lnx+$\frac{1}{x}$>1(填“>“或“<“).分析 构造函数f(x)=lnx+$\frac{1}{x}$,x>1,可得函数单调递增,可得f(x)=lnx+$\frac{1}{x}$>f(1)=1,可得结论.
解答 解:构造函数f(x)=lnx+$\frac{1}{x}$,x>1,
则f′(x)=$\frac{1}{x}$-$\frac{1}{{x}^{2}}$=$\frac{x-1}{{x}^{2}}$>0,
∴函数f(x)=lnx+$\frac{1}{x}$当x>1时单调递增,
∴f(x)=lnx+$\frac{1}{x}$>f(1)=1
故答案为:>
点评 本题考查不等式比较大小,构造函数用导数法研究函数的单调性是解决问题的关键,属基础题.

练习册系列答案
相关题目
12. 函数f(x)=2sin(ωx+φ)(ω>0,0≤φ≤$\frac{π}{2}$)的部分图象如图所示,其中A,B两点之间的距离为5,那么下列说法正确的是( )
函数f(x)=2sin(ωx+φ)(ω>0,0≤φ≤$\frac{π}{2}$)的部分图象如图所示,其中A,B两点之间的距离为5,那么下列说法正确的是( )
 函数f(x)=2sin(ωx+φ)(ω>0,0≤φ≤$\frac{π}{2}$)的部分图象如图所示,其中A,B两点之间的距离为5,那么下列说法正确的是( )
函数f(x)=2sin(ωx+φ)(ω>0,0≤φ≤$\frac{π}{2}$)的部分图象如图所示,其中A,B两点之间的距离为5,那么下列说法正确的是( )| A. | 函数f(x)的最小正周期为8 | |
| B. | f(3)=-$\frac{1}{2}$ | |
| C. | x=-1是函数f(x)的一条对称轴 | |
| D. | 函数f(x)向左平移一个单位长度后所得的函数为偶函数 |
17.函数y=cos(πx+$\frac{π}{6}$)的一个单调增区间是( )
| A. | [-$\frac{2}{3}$,$\frac{1}{3}$] | B. | [$\frac{1}{3}$,$\frac{4}{3}$] | C. | [-$\frac{1}{6}$,$\frac{5}{6}$] | D. | [$\frac{5}{6}$,$\frac{11}{6}$] |
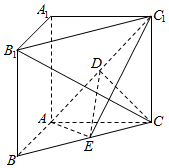 如图,在直三棱柱ABC-A1B1C1中,CC1⊥平面ABC,∠BAC=90°,AB=AC=AA1=2,且E是BC的中点,D是AC1中点.
如图,在直三棱柱ABC-A1B1C1中,CC1⊥平面ABC,∠BAC=90°,AB=AC=AA1=2,且E是BC的中点,D是AC1中点.