题目内容
对于正项数列{an},定义Hn=
为{an}的“给力”值,现知某数列的“给力”值为Hn=
,则数列{an}的通项公式为an=( )
| n |
| a1+2a2+3a3+…+nan |
| 2 |
| n+2 |
A、
| ||
B、
| ||
C、
| ||
D、2n-
|
考点:数列的概念及简单表示法
专题:新定义,点列、递归数列与数学归纳法
分析:根据题意,求出a1+2a2+3a3+…+nan的值,从而得出n-1时的值,两式相减得到an的通项公式.
解答:
解:根据题意,得;
=
,
∴a1+2a2+3a3+…+nan=
,
∴a1+2a2+3a3+…+(n-1)an-1=
;
两式相减,得nan=
,
∴an=
=1+
.
故选:A.
| n |
| a1+2a2+3a3+…+nan |
| 2 |
| n+2 |
∴a1+2a2+3a3+…+nan=
| n(n+2) |
| 2 |
∴a1+2a2+3a3+…+(n-1)an-1=
| (n-1)(n+1) |
| 2 |
两式相减,得nan=
| n(n+2)-(n-1)(n+1) |
| 2 |
∴an=
| 2n+1 |
| 2n |
| 1 |
| 2n |
故选:A.
点评:本题考查了新定义的应用问题,解题时应弄清题意,根据递推公式求出数列的通项公式,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
为得到函数y=sin2x的图象,只需将函数y=cos(x+
)的图象( )
| π |
| 3 |
A、横坐标变为原来2倍,再向右平移
| ||||
B、横坐标变为原来2倍,再向右平移
| ||||
C、横坐标变为原来
| ||||
D、横坐标变为原来
|
已知a,b,c,d∈R,则下列选项正确的是( )
| A、a>b⇒am2>bm2 | ||||
B、
| ||||
| C、a>b,c>d⇒a+c>b+d | ||||
D、a>b⇒
|
设{an}是各项互不相等的正数等差数列,{bn}是各项互不相等的正数等比数列,a1=b1,a2n+1=b2n+1,则( )
| A、an+1>bn+1 |
| B、an+1≥bn+1 |
| C、an+1<bn+1 |
| D、an+1=bn+1 |
已知扇形的周长是12,面积是8,则扇形的中心角的弧度数是( )
| A、1 | B、4 | C、1或4 | D、2或4 |
函数y=f(x)的部分图象如图所示,则y=f(x)的解析式为( )
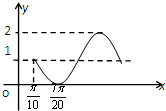

A、y=2sin(2x-
| ||
B、y=sin(2x-
| ||
C、y=2sin(2x+
| ||
D、y=sin(2x+
|
已知a、b为△ABC的边,A、B分别是a、b的对角,且
=
,则
的值=( )
| sinA |
| sinB |
| 2 |
| 3 |
| a+b |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
在公差为4的正项等差数列中,a3与2的算术平均值等于S3与2的几何平均值,其中S3 表示数列的前三项和,则a10为( )
| A、38 | B、40 | C、42 | D、44 |