题目内容
在正方体ABCD-A1B1C1D1中，P，Q分别是AB，B1C1上的点AP=B1Q，N是PQ的中点，M是正方形ABB1A1的中心．求证：（1）MN∥平面A1B1C1D1；
（2）MN∥A1C1．
考点：直线与平面平行的判定,空间中直线与直线之间的位置关系
专题：空间位置关系与距离
分析：（1）要证MN∥平面A1B1C1D1，只需证明MN平行于该平面内的一条直线即可，连结PM并延长交A1B1于G，连结GQ后可得MN平行于GQ，由线面平行的判定即得结论；
（2）由三角形全等可得AP=GB1，则GB1=B1Q，由平行线截线段成比例定理可得GQ∥A1C1，再由平行公理即得结论．
（2）由三角形全等可得AP=GB1，则GB1=B1Q，由平行线截线段成比例定理可得GQ∥A1C1，再由平行公理即得结论．
解答：
证明：（1）如图，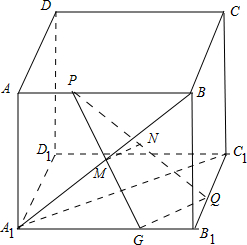
连结PM并延长交A1B1于G，连结GQ，
因为N是PQ的中点，M是正方形ABB1A1的中心，
所以MN∥GQ，
又因为GQ?面A1B1C1D1，MN?面A1B1C1D1，
所以MN∥平面A1B1C1D1；
（2）因为M是正方形ABB1A1的中心，
所以△PBM≌△A1GM，所以AP=GB1，
又AP=B1Q，GB1=B1Q，所以GQ∥A1C1，
又MN∥GQ，所以MN∥A1C1．
连结PM并延长交A1B1于G，连结GQ，
因为N是PQ的中点，M是正方形ABB1A1的中心，
所以MN∥GQ，
又因为GQ?面A1B1C1D1，MN?面A1B1C1D1，
所以MN∥平面A1B1C1D1；
（2）因为M是正方形ABB1A1的中心，
所以△PBM≌△A1GM，所以AP=GB1，
又AP=B1Q，GB1=B1Q，所以GQ∥A1C1，
又MN∥GQ，所以MN∥A1C1．
点评：本题考查直线与平面平行的判定、直线与平面平行的性质以及学生的空间想象能力和思维能力，创设判定定理成立的条件是解答本题的关键，属中档题．
练习册系列答案
相关题目
在△ABC中，若sin2A+sin2C+cos2B＜1，则△ABC一定是（ ）
| A、钝角三角形 | B、直角三角形 |
| C、锐角三角形 | D、不确定 |