若动点P(x.y)在$\frac{x^2}{4}+\frac{y^2}{9}=1$曲线上变化.则x2+2y的最大值为( )A．$\frac{25}{4}$B．$\frac{27}{4}$C．6D．8 题目和参考答案——青夏教育精英家教网—

题目内容

13．若动点P（x，y）在$\frac{x^2}{4}+\frac{y^2}{9}=1$曲线上变化，则x²+2y的最大值为（　　）

A．

$\frac{25}{4}$

B．

$\frac{27}{4}$

C．

D．

分析先设出x=2cosθ，y=3sinθ，再利用三角函数以及二次函数的性质，从而得到答案．

解答解：设x=2cosθ，y=3sinθ，
∴x²+2y
=4cos²θ+6sinθ
=4（1-sin²θ）+6sinθ
=（sinθ-$\frac{3}{4}$）2+$\frac{25}{4}$
≤$\frac{25}{4}$，当且仅当sinθ=$\frac{3}{4}$时取等号．
故选：A．

点评本题考查了椭圆的性质，考查了三角函数以及二次函数的性质，是一道中档题．

练习册系列答案

4．已知{a_n}是首项为1的等比数列，且a₄=8，则数列$\left\{{\frac{1}{a_n}}\right\}$的前5项和为（　　）

1．已知函数$f（x+\frac{1}{2}）$为奇函数，g（x）=f（x）+1，若${a_n}=g（\frac{n}{2016}）$，则数列的前2015项之和为（　　）

8．已知直线l：kx-y+1+2k=0．（k∈R）．
（1）若直线l不经过第四象限，求k的取值范围；
（2）若直线l交x轴负半轴于点A，交y轴正半轴于点B，O为坐标原点，设△AOB的面积为4，求直线l的方程．

18．已知直线l：$\left\{\begin{array}{l}{x=1+\sqrt{3}t}\\{y=\frac{\sqrt{3}}{2}t}\end{array}\right.$（t为参数），曲线C₁：$\left\{\begin{array}{l}{x=2cosθ}\\{y=sinθ}\end{array}\right.$（θ为参数）．
（1）设l与C₁相交于A，B两点，求|AB|；
（2）若把曲线C₁上各点的横坐标压缩为原来的$\frac{1}{2}$，纵坐标压缩为原来的$\frac{{\sqrt{3}}}{2}$得到曲线C₂，设点P是曲线C₂上的一个动点，求它到直线l的距离的最大值．

5．函数f（x）=lnx-|x-2|的零点的个数为2．

2．

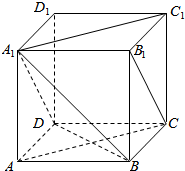如图在正方体ABCD-A₁B₁C₁D₁中，
（1）求证：平面AA₁C₁C⊥平面A₁BD
（2）求直线A₁B与平面A₁B₁CD所成的角．

3．（学法反思总结题）
结合平时学习体会，请回答以下问题：
（1）你认为求二面角常用的方法有哪些？请按应用的重要程度写出3种，并就其中一种方法谈谈它的应用条件；
（2）在解决数学题目时会经常遇到陌生难题，对这些陌生难题的解决往往不知所措，实际上对这些陌生难题的解决方法往往都是通过分析将其转化成为若干常见的基本问题加以解决，也就是我们教师常说的：所谓的难题都是由若干基本题拼凑而成的．请你结合对立体几何问题的解决体会，谈谈对于一个陌生的立体几何难题经常采取哪些策略方法可将其转化为若干常见问题的，要求写出3种策略．

试题分类