题目内容
3.函数$f(x)=sin(x+\frac{π}{6})cos(x+\frac{π}{6})$,给出下列结论:①f(x)的最小正周期为π
②f(x)的一条对称轴为x=$\frac{π}{6}$
③f(x)的一个对称中心为$(\frac{π}{6},0)$
④$f(x-\frac{π}{6})$是奇函数
其中正确结论的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 函数$f(x)=sin(x+\frac{π}{6})cos(x+\frac{π}{6})$=$\frac{1}{2}sin(2x+\frac{π}{3})$,逐一分析四个结论的真假,可得答案.
解答 解:∵函数$f(x)=sin(x+\frac{π}{6})cos(x+\frac{π}{6})$=$\frac{1}{2}sin(2x+\frac{π}{3})$,
∵ω=2,故f(x)的最小正周期为π,故①正确;
当x=$\frac{π}{6}$时,f(x)取最大值,故f(x)的一条对称轴为x=$\frac{π}{6}$,故②正确,③错误;
$f(x-\frac{π}{6})$=$\frac{1}{2}sin2x$,函数图象关于原点对称,是奇函数,故④正确,
故正确的结论有3个,故选:C.
点评 本题考查的知识点是三角函数的周期性,对称性,奇偶性,难度中档.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.已知集合$A=\left\{{\left.x\right|x=\frac{k}{2},k∈Z}\right\},B=\left\{{\left.x\right|x=\frac{k}{4},k∈Z}\right\}$,则( )
| A. | A⊆B | B. | B⊆A | ||
| C. | A=B | D. | A与B的关系不确定 |
13.若动点P(x,y)在$\frac{x^2}{4}+\frac{y^2}{9}=1$曲线上变化,则x2+2y的最大值为( )
| A. | $\frac{25}{4}$ | B. | $\frac{27}{4}$ | C. | 6 | D. | 8 |
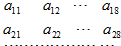 (理)64个正数排成8行8列,如图所示:在符号aij(1≤i≤8,1≤j≤8)中,i表示该数所在的行数,j表示该数所在的列数.已知每一行都成等差数列,而每一列都成等比数列(且每列公比都相等).若a11=$\frac{1}{2}$,a24=1,a32=$\frac{1}{4}$.则a81a82…a88…aij=j($\frac{1}{2}$)i.
(理)64个正数排成8行8列,如图所示:在符号aij(1≤i≤8,1≤j≤8)中,i表示该数所在的行数,j表示该数所在的列数.已知每一行都成等差数列,而每一列都成等比数列(且每列公比都相等).若a11=$\frac{1}{2}$,a24=1,a32=$\frac{1}{4}$.则a81a82…a88…aij=j($\frac{1}{2}$)i.