题目内容
15.关于直线l,m及平面α,β,下列命题中正确的是( )| A. | 若l∥α,α∩β=m,则l∥m | B. | 若l∥α,m∥α,则l∥m | ||
| C. | 若l⊥α,m∥α,则l⊥m | D. | 若l∥α,m⊥l,则m⊥α |
分析 在A中,l与m平行或异面;在B中,l与m相交、平行或异面;在C中,由线面垂直的性质定理得l⊥m;在D中,m与α相交、平行或m?α.
解答 解:由直线l,m及平面α,β,知:
在A中,若l∥α,α∩β=m,则l与m平行或异面,故A错误;
在B中,若l∥α,m∥α,则l与m相交、平行或异面,故B错误;
在C中,若l⊥α,m∥α,则由线面垂直的性质定理得l⊥m,故C正确;
在D中,若l∥α,m⊥l,则m与α相交、平行或m?α,故D错误.
故选:C.
点评 本题考查命题真假的判断,是中档题,解题时要认真审题,注意空间中线线、线面、面面的位置关系的合理运用.

练习册系列答案
相关题目
20.下列四组函数中,表示相等函数的一组是( )
| A. | f(x)=1,g(x)=x0 | B. | f(x)=|x|,g(t)=$\sqrt{{t}^{2}}$ | ||
| C. | f(x)=$\frac{{x}^{2}-1}{x-1}$,g(x)=x+1 | D. | f(x)=lg(x+1)+lg(x-1),g(x)=lg(x2-1) |
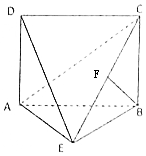 如图,四边形ABCD为矩形,DA⊥平面ABE,AE=EB=BC=2,BF⊥平面ACE于点F,且点F在CE上.
如图,四边形ABCD为矩形,DA⊥平面ABE,AE=EB=BC=2,BF⊥平面ACE于点F,且点F在CE上.


