题目内容
偶函数f（x）的定义域为R，g（x）=f（x-1），g（x）是奇函数，且g（3）=1，则f（2014）=（ ）
| A、0 | B、1 | C、-1 | D、2014 |
考点：函数奇偶性的性质,函数的值
专题：函数的性质及应用
分析：根据g（x）是奇函数及已知条件得到f（x+1）=-f（x-1），即f（x-1）=-f（x+1），所以f（x）=-f（x+2）=f（x+4），所以函数f（x）的周期是4，所以f（2014）=f（2+503×4）=f（2），所以根据已知条件求f（2）即可．
解答：
解：∵g（x）是奇函数，∴g（-x）=f（-x-1）=-g（x）=-f（x-1）；
又f（x）是偶函数，∴f（x+1）=-f（x-1），即f（x-1）=-f（x+1），∴f（x）=-f（x+2）=f（x+4）；
∴f（x）是周期为4的周期函数；
∴f（2014）=f（2+503×4）=f（2）=g（3）=1．
故选B．
又f（x）是偶函数，∴f（x+1）=-f（x-1），即f（x-1）=-f（x+1），∴f（x）=-f（x+2）=f（x+4）；
∴f（x）是周期为4的周期函数；
∴f（2014）=f（2+503×4）=f（2）=g（3）=1．
故选B．
点评：考查奇偶函数的定义，以及函数周期的概念．
练习册系列答案
名校课堂系列答案
相关题目
在△ABC中，若
=
=
，则△ABC是（ ）
| cosA |
| cosB |
| b |
| a |
| 4 |
| 3 |
| A、等腰三角形 |
| B、直角三角形 |
| C、等腰或直角三角形 |
| D、钝角三角形 |
已知二次函数f（x）=ax2+bx+c，不等式f（x）＞-2x的解集为{x|1＜x＜3}．
（Ⅰ）若方程f（x）=2a有两个相等正根，求f（x）的解析式；
（Ⅱ）若f（x）的最大值为正数，求a的取值范围．
（Ⅰ）若方程f（x）=2a有两个相等正根，求f（x）的解析式；
（Ⅱ）若f（x）的最大值为正数，求a的取值范围．
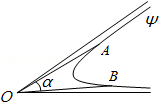如图，对于曲线Ψ所在平面内的点O，若存在以O为顶点的角α，使得α≥∠AOB对于曲线Ψ上的任意两个不同的点A、B恒成立，则称角α为曲线Ψ的相对于点O的“界角”，并称其中最小的“界角”为曲线Ψ的相对于点O的“确界角”．已知曲线C：f（x）=