题目内容
已知函数f(x)=alnx+
+x.(a≠0).
(1)若曲线y=f(x)在点(1,f(1))处的切线与直线x-2y=0垂直,求实数a的值;
(2)若a>0,求f(x)的最小值g(a);
(3)在(2)的基础上求证:g(a)≥-e-4.
| 2a2 |
| x |
(1)若曲线y=f(x)在点(1,f(1))处的切线与直线x-2y=0垂直,求实数a的值;
(2)若a>0,求f(x)的最小值g(a);
(3)在(2)的基础上求证:g(a)≥-e-4.
考点:利用导数研究曲线上某点切线方程,导数在最大值、最小值问题中的应用
专题:导数的综合应用
分析:(1)求出原函数的导函数,根据曲线y=f(x)在点(1,f(1))处的切线与直线x-2y=0垂直,可得f′(1)=-2,由此可得实数a的值;
(2)求出原函数的导函数,由导函数的符号确定原函数的单调区间,求出极值点,得到极小值即最小值;
(3)对(2)中求出的g(a)求导,利用导数求其最小值,即可证得g(a)≥-e-4.
(2)求出原函数的导函数,由导函数的符号确定原函数的单调区间,求出极值点,得到极小值即最小值;
(3)对(2)中求出的g(a)求导,利用导数求其最小值,即可证得g(a)≥-e-4.
解答:
(1)解:f(x)的定义域为{x|x>0},f′(x)=
-
+1(x>0),
根据题意,有f′(1)=-2,
∴2a2-a-3=0,解得a=-1或a=
;
(2)解:由(1)得,f′(x)=
(x>0).
当a>0时,∵x>0,
由f′(x)>0得(x-a)(x+2a)>0,解得x>a;
由f′(x)<0得(x-a)(x+2a)<0,解得0<x<a.
∴函数f(x)在(a,+∞)上单调递增,在(0,a)上单调递减.
∴f(x)在(0,+∞)上有极小值,也就是最小值为g(a)=a(lna+3);
(3)证明:由(2)知,g(a)=a(lna+3),
g′(a)=lna+3+a•
=lna+4.
令g′(a)=0,得a=e-4.
当0<a<e-4时,g′(a)<0,函数g(a)在(0,e-4)上为减函数;
当a>e-4时,g′(a)>0,函数g(a)在(e-4,+∞)上为增函数.
∴g(a)在(0,+∞)上有唯一极值点,且是极小值点,从而也是g(a)的最小值点.
∴g(a)min=e-4(lne-4+3)=-e-4.
∴g(a)≥-e-4.
| a |
| x |
| 2a2 |
| x2 |
根据题意,有f′(1)=-2,
∴2a2-a-3=0,解得a=-1或a=
| 3 |
| 2 |
(2)解:由(1)得,f′(x)=
| (x-a)(x+2a) |
| x2 |
当a>0时,∵x>0,
由f′(x)>0得(x-a)(x+2a)>0,解得x>a;
由f′(x)<0得(x-a)(x+2a)<0,解得0<x<a.
∴函数f(x)在(a,+∞)上单调递增,在(0,a)上单调递减.
∴f(x)在(0,+∞)上有极小值,也就是最小值为g(a)=a(lna+3);
(3)证明:由(2)知,g(a)=a(lna+3),
g′(a)=lna+3+a•
| 1 |
| a |
令g′(a)=0,得a=e-4.
当0<a<e-4时,g′(a)<0,函数g(a)在(0,e-4)上为减函数;
当a>e-4时,g′(a)>0,函数g(a)在(e-4,+∞)上为增函数.
∴g(a)在(0,+∞)上有唯一极值点,且是极小值点,从而也是g(a)的最小值点.
∴g(a)min=e-4(lne-4+3)=-e-4.
∴g(a)≥-e-4.
点评:本题考查了利用导数研究过曲线上某点处的切线方程,考查了利用导数研究函数的最值,考查了计算能力,是压轴题.

练习册系列答案
 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
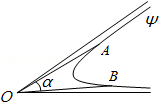 如图,对于曲线Ψ所在平面内的点O,若存在以O为顶点的角α,使得α≥∠AOB对于曲线Ψ上的任意两个不同的点A、B恒成立,则称角α为曲线Ψ的相对于点O的“界角”,并称其中最小的“界角”为曲线Ψ的相对于点O的“确界角”.已知曲线C:f(x)=
如图,对于曲线Ψ所在平面内的点O,若存在以O为顶点的角α,使得α≥∠AOB对于曲线Ψ上的任意两个不同的点A、B恒成立,则称角α为曲线Ψ的相对于点O的“界角”,并称其中最小的“界角”为曲线Ψ的相对于点O的“确界角”.已知曲线C:f(x)=
|
A、
| ||
B、
| ||
C、
| ||
D、
|
已知圆C:x2+(y-3)2=9,过原点作圆C的弦OP,则OP的中点Q的轨迹方程为( )
A、(x-
| ||||
B、(x-
| ||||
C、x2+(y-
| ||||
D、x2+(y-
|