题目内容
已知函数f(x)=ax2-(a+1)x+1,a∈R.
(1)求证:函数f(x)的图象与x轴有交点;
(2)当a>0时,求函数y=
的定义域;
(3)若存在m>0使关于x的方程f(|x|)=m+
有四个不同的实根,求实数a的取值范围.
(1)求证:函数f(x)的图象与x轴有交点;
(2)当a>0时,求函数y=
| f(x) |
(3)若存在m>0使关于x的方程f(|x|)=m+
| 1 |
| m |
考点:二次函数的性质
专题:函数的性质及应用
分析:(1)利用分类讨论思想证明函数与x轴的交点.
(2)进一步利用分类讨论思想求函数的定义域.
(3)根据方程有四个交点确定
最后解不等式组求的结果.
(2)进一步利用分类讨论思想求函数的定义域.
(3)根据方程有四个交点确定
|
解答:
证明:(1)已知函数f(x)=ax2-(a+1)x+1,a∈R.
①当a=0时,f(x)=-x+1,
则与x轴的交点坐标为:(1,0);
②当a>0时,函数f(x)为开口方向向上的抛物线,
则:△=(a+1)2-4a=(a-1)2≥0;
③当a<0时,函数f(x)为开口方向向下的抛物线,
则:△=(a+1)2-4a=(a-1)2≥0;
综上所述:函数f(x)的图象与x轴有交点;
解:(2)当a>0时,y=
=
①当a=1时,y=
=
=
,
所以x∈R;
②当0<a<1时,y=
=
=
,
则x的定义域为:{x|x>
或x<1};
③当a>1时,
y=
=
=
,
则x的定义域为:{x|x>1或x<
};
解:(3)令t=m+
≥2,
则:关于x的方程f(|x|)=t有四个不等的实数根.
即:a|x|2+(a+1)|x|+1-t=0有四个不等的实数根.
即:ax2+(a+1)x+1-t=0有两个正根.
则:
,
解得:a<-1.
①当a=0时,f(x)=-x+1,
则与x轴的交点坐标为:(1,0);
②当a>0时,函数f(x)为开口方向向上的抛物线,
则:△=(a+1)2-4a=(a-1)2≥0;
③当a<0时,函数f(x)为开口方向向下的抛物线,
则:△=(a+1)2-4a=(a-1)2≥0;
综上所述:函数f(x)的图象与x轴有交点;
解:(2)当a>0时,y=
| f(x) |
| ax2-(a+1)x+1 |
①当a=1时,y=
| f(x) |
| ax2-(a+1)x+1 |
| (x-1)2 |
所以x∈R;
②当0<a<1时,y=
| f(x) |
| ax2-(a+1)x+1 |
| (ax-1)(x-1) |
则x的定义域为:{x|x>
| 1 |
| a |
③当a>1时,
y=
| f(x) |
| ax2-(a+1)x+1 |
| (ax-1)(x-1) |
则x的定义域为:{x|x>1或x<
| 1 |
| a |
解:(3)令t=m+
| 1 |
| m |
则:关于x的方程f(|x|)=t有四个不等的实数根.
即:a|x|2+(a+1)|x|+1-t=0有四个不等的实数根.
即:ax2+(a+1)x+1-t=0有两个正根.
则:
|
解得:a<-1.
点评:本题考查的知识要点:函数的分类讨论的应用,函数的定义域,及函数的根的情况.属于中等题型.

练习册系列答案
相关题目
已知三点A(3,1)、B(-2,k)、C(8,11)共线,则k的取值是( )
| A、-6 | B、-7 | C、-8 | D、-9 |
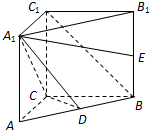 如图,在直三棱柱ABC-A1B1C1中,∠ACB=
如图,在直三棱柱ABC-A1B1C1中,∠ACB=