题目内容
3.不等式|3x-2|>1的解集为( )| A. | (-∞,-$\frac{1}{3}$)∪(1,+∞) | B. | (-$\frac{1}{3}$,1) | C. | (-∞,$\frac{1}{3}$)∪(1,+∞) | D. | ($\frac{1}{3}$,1) |
分析 原不等式等价于 3x-2<-1,或 3x-2>1,求得x的范围,可得原不等式的解集.
解答 解:不等式|3x-2|>1等价于 3x-2<-1,或 3x-2>1,
求得x<$\frac{1}{3}$,或x>1,故原不等式的解集为{x|x<$\frac{1}{3}$,或x>1},
故选:C.
点评 本题主要考查绝对值不等式的解法,体现了转化的数学思想,属于基础题.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
8.已知不等式9ax+8≥$\frac{36x}{2{x}^{2}+1}$+1在[$\frac{1}{2}$,+∞)上恒成立,则实数a的取值范围是( )
| A. | ($\frac{8}{9}$,+∞) | B. | (-∞,$\frac{8}{9}$) | C. | [$\frac{8}{9}$,+∞) | D. | (-∞,$\frac{8}{9}$] |
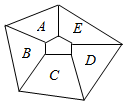 如图,在A,B,C,D,E五个区域中栽种3种植物,要求同一区域中只种1种植物,相邻两区域所种植物不同,则不同的栽种方法的总数为( )
如图,在A,B,C,D,E五个区域中栽种3种植物,要求同一区域中只种1种植物,相邻两区域所种植物不同,则不同的栽种方法的总数为( )