题目内容
20．已知点P（x，y）的坐标满足$\left\{\begin{array}{l}{x+y-4≤0}\\{1≤x≤2}\\{y≥0}\end{array}\right.$则z=x+2y的最大值为（ ）| A． | 4 | B． | 5 | C． | 6 | D． | 7 |
分析 由约束条件作出可行域，化目标函数为直线方程的斜截式，数形结合得到最优解，联立方程组求得最优解的坐标，代入目标函数得答案．
解答 解：由约束条件$\left\{\begin{array}{l}{x+y-4≤0}\\{1≤x≤2}\\{y≥0}\end{array}\right.$作出可行域如图，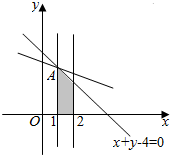
联立$\left\{\begin{array}{l}{x=1}\\{x+y-4=0}\end{array}\right.$，得A（1，3），
化目标函数z=x+2y为y=-$\frac{1}{2}x+\frac{z}{2}$，
由图可知，当直线y=-$\frac{1}{2}x+\frac{z}{2}$过A时，直线在y轴上的截距最大，z最大为1+2×3=7．
故选：D．
点评 本题考查简单的线性规划，考查了数形结合的解题思想方法，是中档题．
练习册系列答案
云南师大附小一线名师提优作业系列答案
相关题目
3．不等式|3x-2|＞1的解集为（ ）
| A． | （-∞，-$\frac{1}{3}$）∪（1，+∞） | B． | （-$\frac{1}{3}$，1） | C． | （-∞，$\frac{1}{3}$）∪（1，+∞） | D． | （$\frac{1}{3}$，1） |
8．已知函数f（x）=|log4x|，正实数m、n满足m＜n，且f（m）=f（n），若f（x）在区间[m5，n]上的最大值为5，则m、n的值分别为（ ）
| A． | $\frac{1}{2}$、2 | B． | $\frac{1}{4}$、4 | C． | $\frac{1}{4}$、2 | D． | $\frac{1}{2}$、4 |
5．已知数列{an}为等比数列，且a4•a6=2a5，设等差数列{bn}的前n项和为Sn，若b5=2a5，则S9=（ ）
| A． | 36 | B． | 27 | C． | 54 | D． | 45 |
12．若a=ln2，b=5${\;}^{-\frac{1}{2}}$，c=sin30°，则a，b，c的大小关系（ ）
| A． | a＜b＜c | B． | b＜a＜c | C． | b＜c＜a | D． | c＜b＜a |
9．函数y=$\sqrt{sin（\frac{π}{3}-2x）}$的单调增区间是（ ）
| A． | [k$π-\frac{π}{12}$，k$π+\frac{π}{6}$]，k∈Z | B． | [k$π-\frac{π}{3}$，k$π-\frac{π}{12}$]，k∈Z | ||
| C． | [k$π-\frac{π}{12}$，k$π+\frac{5π}{12}$]，k∈Z | D． | [k$π+\frac{5π}{12}$，k$π+\frac{11π}{12}$]，k∈Z |