题目内容
已知sinx+cosx=
,x∈[
,
],则sinx-cosx等于( )
| 7 |
| 5 |
| π |
| 4 |
| 3π |
| 4 |
A、±
| ||
B、-
| ||
C、
| ||
D、
|
考点:同角三角函数基本关系的运用
专题:三角函数的求值
分析:首先,根据sinx+cosx=
,得到sinxcosx=
>0,然后得到x∈[
,
),从而得到sinx-cosx>0,然后,再计算结果即可.
| 7 |
| 5 |
| 12 |
| 25 |
| π |
| 4 |
| π |
| 2 |
解答:
解:∵sinx+cosx=
,
∴1+2sinxcosx=
,
∴2sinxcosx=
,
∴sinxcosx=
>0,
∴x∈[
,
),
∴sinx-cosx>0,
∴sinx-cosx=
=
=
=
,
∴sinx-cosx=
.
故选:D.
| 7 |
| 5 |
∴1+2sinxcosx=
| 49 |
| 25 |
∴2sinxcosx=
| 24 |
| 25 |
∴sinxcosx=
| 12 |
| 25 |
∴x∈[
| π |
| 4 |
| π |
| 2 |
∴sinx-cosx>0,
∴sinx-cosx=
| (sinx-cosx)2 |
=
| 1-2sinxcosx |
=
1-
|
=
| 1 |
| 5 |
∴sinx-cosx=
| 1 |
| 5 |
故选:D.
点评:本题重点考查了同角三角函数基本关系式、三角函数在各个象限的符号等知识,属于基础题.

练习册系列答案
相关题目
cos(-
π)的值是( )
| 43 |
| 6 |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
已知sin(
+α)=
,则cosα的值为( )
| 5π |
| 2 |
| 2 |
| 5 |
A、
| ||||
B、-
| ||||
C、±
| ||||
D、±
|
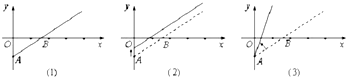 如图(1)是反应某公共汽车线路收支差额(即营运所得票价收入与付出成本的差)y与乘客两x之间关系的图象.由于目前该条公交线亏损,公司有关人员提出了两种调整的建议,如图(2)(3)的实线(虚线为原参考线)所示.给出下列说法:
如图(1)是反应某公共汽车线路收支差额(即营运所得票价收入与付出成本的差)y与乘客两x之间关系的图象.由于目前该条公交线亏损,公司有关人员提出了两种调整的建议,如图(2)(3)的实线(虚线为原参考线)所示.给出下列说法: