题目内容
已知|
|=3，|
|=5，
与
的夹角为120°．
试求：（1）
2-
2；
（2）|2
+
|；
（3）(
-
)•(3
+
)．
| a |
| b |
| a |
| b |
试求：（1）
| a |
| b |
（2）|2
| a |
| b |
（3）(
| a |
| b |
| a |
| b |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：（1）直接代入即可得出；
（2）
•
=3×5×cos120°=-
，再利用数量积运算性质即可得出|2
+
|=
．
（3）利用数量积运算性质展开可得(
-
)•(3
+
)=3
2-
2-2
•
．
（2）
| a |
| b |
| 15 |
| 2 |
| a |
| b |
4
|
（3）利用数量积运算性质展开可得(
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
解答：
解：（1）
2-
2=|
|2-|
|2=32-52=-16；
（2）∵|
|=3，|
|=5，
与
的夹角为120°．
∴
•
=3×5×cos120°=-
，
∴|2
+
|=
=
=
．
（3）(
-
)•(3
+
)=3
2-
2-2
•
=3×32-52-2×(-
)=17．
| a |
| b |
| a |
| b |
（2）∵|
| a |
| b |
| a |
| b |
∴
| a |
| b |
| 15 |
| 2 |
∴|2
| a |
| b |
4
|
4×32+52-4×
|
| 31 |
（3）(
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| 15 |
| 2 |
点评：本题考查了数量积的运算性质，考查了计算能力，属于中档题．
练习册系列答案
举一反三期末百分冲刺卷系列答案
相关题目
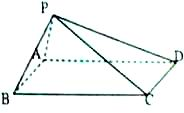如图，四棱锥P-ABCD的底面ABCD是矩形，且AB=2，BC=
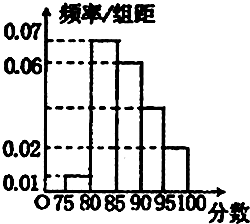某高校在今年的自主招生考试成绩中随机抽取100名考生的笔试成绩，分为5组制出频率分布直方图如图所示．（1）求a，b，c，d；（2）该校决定在成绩较好的3，4，5组用分层抽样抽取6名学生进行面试，则每组应各抽多少名学生？已知O是△ABC所在平面内一点，且|
|2+|
|2=|
|2+|
|2=|
|2+|
|2，则O是△ABC的（ ）
| OC |
| AB |
| OB |
. |
| AC |
| OA |
| BC |
| A、内心 | B、垂心 | C、外心 | D、重心 |
一个几何体的三视图如图所示，则该几何体的体积为（ ）
A、8+
| ||||
B、8+2
| ||||
| C、12 | ||||
D、
|