题目内容
已知函数f(x)=
,若对任意的x∈R,不等式f(x)≤m2-
m恒成立,则实数m的取值范围是( )
|
| 3 |
| 4 |
A、(-∞,-
| ||
B、(-∞,-
| ||
| C、[1,+∞) | ||
D、[-
|
考点:分段函数的应用
专题:计算题,函数的性质及应用,不等式的解法及应用
分析:求出分段函数的最大值,把不等式f(x)≤m2-
m恒成立转化为m2-
m大于等于f(x)的最大值恒成立,然后求解不等式得到实数m的取值范围.
| 3 |
| 4 |
| 3 |
| 4 |
解答:
解:对于函数f(x)=
,
当x≤1时,f(x)=-(x-
)2+
≤
;
当x>1时,f(x)=log
x<0.
则函数f(x)的最大值为
.
则要使不等式f(x)≤m2-
m恒成立,
则m2-
m≥
恒成立,即m≤-
或m≥1.
故选B.
|
当x≤1时,f(x)=-(x-
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
当x>1时,f(x)=log
| 1 |
| 3 |
则函数f(x)的最大值为
| 1 |
| 4 |
则要使不等式f(x)≤m2-
| 3 |
| 4 |
则m2-
| 3 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
故选B.
点评:本题考查了恒成立问题,训练了分段函数的最值的求法,考查了数学转化思想方法,考查运算能力,是中档题.

练习册系列答案
相关题目
已知中心在原点,焦点在y轴上的双曲线的离心率为
,则它的渐近线方程为( )
| 5 |
| A、y=±2x | ||||
B、y=±
| ||||
C、y=±
| ||||
D、y=±
|
已知函数f(x)=(
)x-log
x,若实数x0是方程f(x)=0的解,且0<x1<x0,则f(x1)的值( )
| 1 |
| 5 |
| 1 |
| 3 |
| A、恒为负 | B、等于零 |
| C、恒为正 | D、不大于零 |
设[x]表示不超过x的最大整数(如[2]=2,[
]=1).对于给定的n∈N*,定义Cnx=
,x∈[1,+∞),则当x∈[
,3)时,函数f(x)=C8x的值域为( )
| 3 |
| 2 |
| n(n-1)…(n-[x]+1) |
| x(x-1)…(x-[x]+1) |
| 5 |
| 4 |
A、(4,
| ||||
B、(4,
| ||||
C、[4,
| ||||
D、[
|
 如图,在半径为3的圆O中,直径AB与弦CD垂直,垂足为E(E在A、O之间).若CE=
如图,在半径为3的圆O中,直径AB与弦CD垂直,垂足为E(E在A、O之间).若CE= 如图所示,PA⊥平面ABCD,四边形ABCD为正方形,且E,F,G,H分别是线段PA、PD、CD、BC的中点.
如图所示,PA⊥平面ABCD,四边形ABCD为正方形,且E,F,G,H分别是线段PA、PD、CD、BC的中点.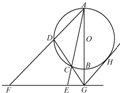 如图,AB是圆O的直径,G是AB延长线上的一点,GCD是圆O的割线,过点G作AG的垂线,交直线AC于点E,交直线 AD于点F,过点G作圆O的切线,切点为H.
如图,AB是圆O的直径,G是AB延长线上的一点,GCD是圆O的割线,过点G作AG的垂线,交直线AC于点E,交直线 AD于点F,过点G作圆O的切线,切点为H.