题目内容
某足够大德长方体箱子放置一球O,已知球O与长方体一个顶点出发的三个平面都相切,且球面上一点M到三个平面的距离分别为3,2,1,求球的半径.
考点:球的体积和表面积
专题:计算题,空间位置关系与距离
分析:设(a,b,c) 为球心,半径为R球面方程(x-a)2+(x-b)2+(x-c)2=R2,由于球与三个平面相切,所以有:半径R=|a|=|b|=|c|另外,球面上某点M(3,2,1),当然在球面上,并且到三个平面的距离分别为3、2、1,所以:(3-R)2+(2-R)2+(1-R)2=R2,即可得出结论.
解答:
解:设(a,b,c) 为球心,半径为R球面方程(x-a)2+(x-b)2+(x-c)2=R2
由于球与三个平面相切,所以有:半径R=|a|=|b|=|c|
另外,球面上某点M(3,2,1),当然在球面上,并且到三个平面的距离分别为3、2、1,
所以:(3-R)2+(2-R)2+(1-R)2=R2,
即 2R2-12R+14=0
R2-6R+9=(R-3)2=2
解得:R=3±
,
由于球与三个平面相切,所以有:半径R=|a|=|b|=|c|
另外,球面上某点M(3,2,1),当然在球面上,并且到三个平面的距离分别为3、2、1,
所以:(3-R)2+(2-R)2+(1-R)2=R2,
即 2R2-12R+14=0
R2-6R+9=(R-3)2=2
解得:R=3±
| 2 |
点评:本题考查平面与球相切,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
定义域是R上的函数f(x)满足f(x+2)=2f(x),当x∈(0,2]时,f(x)=
,若x∈(-4,-2]时,f(x)≤
-
有解,则实数t的取值范围是( )
|
| t |
| 4 |
| 1 |
| 2t |
| A、[-2,0)∪(0,1) |
| B、[-2,0)∪[1,+∞) |
| C、[-2,1] |
| D、(-∞,-2]∪(0,1] |
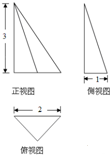 某三棱锥的三视图如图所示,其正视图和侧视图都是直角三角形,则该三棱锥的体积等于( )
某三棱锥的三视图如图所示,其正视图和侧视图都是直角三角形,则该三棱锥的体积等于( )A、
| ||
B、
| ||
| C、1 | ||
| D、3 |
函数f(x)=2x2-2x-1的零点个数为( )
| A、0个 | B、1个 | C、2个 | D、不确定 |

