题目内容
3.函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的一部分图象如图所示,试确定函数的解析式.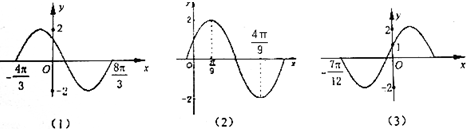
分析 根据函数的图象,得出最大值A,由周期T求出ω,再把图象中的点的坐标代人函数解析式求出φ的值即可.
解答 解:(1)根据函数的图象,知;最大值为A=2,
周期为T=$\frac{8π}{3}$-(-$\frac{4π}{3}$)=4π,∴ω=$\frac{1}{2}$;
又x=-$\frac{4π}{3}$时,y=2sin($\frac{1}{2}$x+φ)=0,
∴$\frac{1}{2}$x+φ=2kπ,k∈Z,
∴φ=4kπ+$\frac{2π}{3}$,k∈Z,
又|φ|<π,∴φ=$\frac{2π}{3}$,
∴y=2sin($\frac{1}{2}$x+$\frac{2π}{3}$);
(2)根据函数的图象,知;最大值为A=2,
设周期为T,则$\frac{1}{2}$T=$\frac{4π}{9}$-$\frac{π}{9}$=$\frac{1}{3}$π,
∴T=$\frac{2π}{ω}$=$\frac{2π}{3}$,ω=3;
又x=$\frac{π}{9}$时,y=2sin(3x+φ)=2,
∴3×$\frac{π}{9}$+φ=$\frac{π}{2}$+2kπ,k∈Z,
∴φ=2kπ+$\frac{π}{6}$,k∈Z;
又|φ|<π,∴φ=$\frac{π}{6}$,
∴y=2sin(3x+$\frac{π}{6}$);
(3)根据函数的图象,知;最大值为A=2,
又x=0时,y=2sin(ωx+φ)=1,
∴φ=2kπ+$\frac{π}{6}$,k∈Z,
又|φ|<π,∴φ=$\frac{π}{6}$,
∴y=2sin(ωx+$\frac{π}{6}$);
设周期为T,则$\frac{\frac{π}{6}-(-π)}{2π}$T=0-(-$\frac{7π}{12}$)=$\frac{7π}{12}$,
∴T=π,∴ω=2;
∴y=2sin(2x+$\frac{π}{6}$);
点评 本题考查了根据三角函数的部分图象求y=Asin(ωx+φ)解析式的应用问题,是基础题目.

| A. | 1个白球2个红球 | B. | 2个白球1个红球 | C. | 3个都是红球 | D. | 至少有一个红球 |
| A. | $\frac{3}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
| A. | $\frac{3}{2}$ | B. | -$\frac{3}{2}$ | C. | $\frac{8}{3}$ | D. | -$\frac{8}{3}$ |