题目内容
8．已知$\overrightarrow{OA}$=（1，3），$\overrightarrow{OB}$=（-1，1），$\overrightarrow{OC}$=（5，-1），则△ABC经向量$\overrightarrow{a}$=（2，1）平移后得三角形A′B′C′，求$\overrightarrow{OA′}$+$\overrightarrow{OB′}$+$\overrightarrow{OC′}$．分析 利用$\overrightarrow{O{A}^{′}}$=$\overrightarrow{OA}+\overrightarrow{a}$=（3，4），同理可得$\overrightarrow{OB′}$，$\overrightarrow{OC′}$．
解答 解：$\overrightarrow{O{A}^{′}}$=$\overrightarrow{OA}+\overrightarrow{a}$=（3，4），
同理可得$\overrightarrow{OB′}$=（1，2），$\overrightarrow{OC′}$=（7，0）．
∴$\overrightarrow{OA′}$+$\overrightarrow{OB′}$+$\overrightarrow{OC′}$=（3，4）+（1，2）+（7，0）=（11，6）．
点评 本题考查了向量的三角形法则，考查了推理能力与计算能力，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
18．
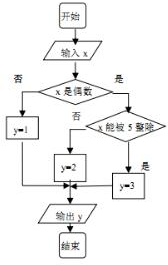某算法的程序图如图所示，其中输入的变量x在1，2，3，…，30这30个整数中等可能随机产生．
（1）分别求出按程序框图正确编程运行时输出y的值为i的概率Pi（i=1，2，3）；
（2）甲、乙两同学依据自己对程序框图的理解，各自编写程序重复运行n次后，统计记录了输出y的值为i（i=1，2，3）的频数，下面是甲、乙所作频数统计表的部分数据：
甲的频数统计表（部分）
乙的频数统计表（部分）
当n=2000时，根据表中的数据，分别写出甲、乙所编程序各自输出y的值为i（i=1，2，3）的频率（用分数表示），并判断甲、乙中谁所编写的程序符合算法要求的可能性较大．
某算法的程序图如图所示，其中输入的变量x在1，2，3，…，30这30个整数中等可能随机产生．（1）分别求出按程序框图正确编程运行时输出y的值为i的概率Pi（i=1，2，3）；
（2）甲、乙两同学依据自己对程序框图的理解，各自编写程序重复运行n次后，统计记录了输出y的值为i（i=1，2，3）的频数，下面是甲、乙所作频数统计表的部分数据：
甲的频数统计表（部分）
| 运行次数 | 输出y=1的频数 | 输出y=2的频数 | 输出y=3的频数 |
| 50 | 24 | 19 | 7 |
| … | … | … | … |
| 2000 | 1027 | 776 | 197 |
| 运行次数 | 输出y=1的频数 | 输出y=2的频数 | 输出y=3的频数 |
| 50 | 26 | 11 | 13 |
| … | … | … | … |
| 2000 | 1051 | 396 | 553 |
13．已知函数f（x）=$\frac{1}{2}$sin2ωx+$\frac{\sqrt{3}}{2}$cos2ωx的最小正周期为π，则f（x）在闭区间[0，$\frac{π}{4}$]的最大值为1．
20．设直线l过坐标原点，它的倾斜角为45°，如果将l绕坐标原点按顺时向旋转60°，得到直线l1，那么l1的倾斜角为（ ）
| A． | 45° | B． | 15° | C． | 105° | D． | 165° |
17．已知命题p：?x∈（0，+∞），2x＞log3x，命题q：?x0∈（0，+∞），sinx0=lnx0，则下列命题中的真命题是（ ）
| A． | （￢p）∨（￢q） | B． | （￢p）∧（￢q） | C． | （￢p）∧q | D． | p∧q |