题目内容
15.已知向量$\overrightarrow{b}$=$\overrightarrow{4{e}_{1}}$+$\overrightarrow{3{e}_{2}}$,其中$\overrightarrow{{e}_{1}}$=(1,0),$\overrightarrow{{e}_{2}}$=(0,1),若$\overrightarrow{c}$=(x,-2),且$\overrightarrow{b}$⊥$\overrightarrow{c}$,则x的值为( )| A. | $\frac{3}{2}$ | B. | -$\frac{3}{2}$ | C. | $\frac{8}{3}$ | D. | -$\frac{8}{3}$ |
分析 求出$\overrightarrow{b}$的坐标,根据$\overrightarrow{b}⊥\overrightarrow{c}$列方程解出x.
解答 解:$\overrightarrow{b}$=(4,3),
∵$\overrightarrow{b}$⊥$\overrightarrow{c}$,∴4x-6=0,解得x=$\frac{3}{2}$.
故选:A.
点评 本题考查了平面向量坐标运算,数量积运算,属于基础题.

练习册系列答案
相关题目
20.设直线l过坐标原点,它的倾斜角为45°,如果将l绕坐标原点按顺时向旋转60°,得到直线l1,那么l1的倾斜角为( )
| A. | 45° | B. | 15° | C. | 105° | D. | 165° |
3.已知复数z=1+i(i是虚数单位),则$\frac{4-2i}{z}$的共轭复数是( )
| A. | -1+3i | B. | 1+3i | C. | 1-3i | D. | -1-3i |
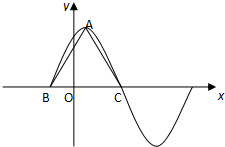 已知f(x)=3cos2$\frac{ωx}{2}$+$\frac{\sqrt{3}}{2}$sinωx-$\frac{3}{2}$(ω>0)在一个周期内的图象如图所示,点A为图象的最高点,B,C为图象与x轴的交点,且三角形ABC的面积为$\frac{\sqrt{3}}{4}$π.
已知f(x)=3cos2$\frac{ωx}{2}$+$\frac{\sqrt{3}}{2}$sinωx-$\frac{3}{2}$(ω>0)在一个周期内的图象如图所示,点A为图象的最高点,B,C为图象与x轴的交点,且三角形ABC的面积为$\frac{\sqrt{3}}{4}$π.