题目内容
11．若tan（α+$\frac{π}{4}$）=3，则tanα=$\frac{1}{2}$．分析 直接使用两角差的正切公式计算．
解答 解：tanα=tan[（α+$\frac{π}{4}$）-$\frac{π}{4}$]=$\frac{tan（α+\frac{π}{4}）-tan\frac{π}{4}}{1+tan（α+\frac{π}{4}）tan\frac{π}{4}}$=$\frac{3-1}{1+3×1}=\frac{1}{2}$．
故答案为：$\frac{1}{2}$．
点评 本题考查了两角和差的正切函数，属于基础题．
练习册系列答案
作业辅导系列答案
同步学典一课多练系列答案
经典密卷系列答案
金牌课堂练系列答案
相关题目
1．
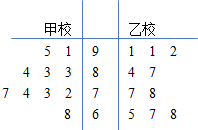为了解高一新生数学基础，甲、乙两校对高一新生进行了数学测试．现从两校各随机抽取10名新生的成绩作为样本，他们的测试成绩的茎叶图如下：
（1）比较甲、乙两校新生的数学测试样本成绩的平均值及方差的大小；（只需要写出结论）
（2）如果将数学基础采用A、B、C等级制，各等级对应的测试成绩标准如表：（满分100分，所有学生成绩均在60分以上）
假设每个新生的测试成绩互相独立．根据所给数据，以事件发生的频率作为相应事件发生的概率．
从甲、乙两校新生中各随机抽取一名新生，求甲校新生的数学基础等级高于乙校新生的数学基础等级的概率．
为了解高一新生数学基础，甲、乙两校对高一新生进行了数学测试．现从两校各随机抽取10名新生的成绩作为样本，他们的测试成绩的茎叶图如下：（1）比较甲、乙两校新生的数学测试样本成绩的平均值及方差的大小；（只需要写出结论）
（2）如果将数学基础采用A、B、C等级制，各等级对应的测试成绩标准如表：（满分100分，所有学生成绩均在60分以上）
| 测试成绩 | [85，100] | [70，85） | （60，70） |
| 基础等级 | A | B | C |
从甲、乙两校新生中各随机抽取一名新生，求甲校新生的数学基础等级高于乙校新生的数学基础等级的概率．
20．设直线l过坐标原点，它的倾斜角为45°，如果将l绕坐标原点按顺时向旋转60°，得到直线l1，那么l1的倾斜角为（ ）
| A． | 45° | B． | 15° | C． | 105° | D． | 165° |
