题目内容

如图所示，AB为⊙O直径，CD切⊙O于D，AB延长线交CD于点C，若∠CAD=25°，则∠C为（　　）
A、45°B、40°
C、35°D、30°
考点：与圆有关的比例线段
专题：直线与圆
分析：利用弦切角定理和三角形内角和定理求解．
解答： 解：连结BD，
∵AB为⊙O直径，CD切⊙O于D，
AB延长线交CD于点C，∠CAD=25°，
∴∠CDB=∠CAD=25°，∠ADB=90°，
∴∠CBD=25°+90°=115°，
∴∠C=180°-115°-25°=40°．
故选：B．
点评：本题考查角的大小的求法，是中档题，解题时要认真审题，注意弦切角定理的合理运用．
练习册系列答案
相关题目
已知命题“?p∨?q是假命题，给出下列四个结论：
（1）命题p∧q为真   
（2）命题p∧q为假 
（3）命题p∨q为真  
（4）命题p∨q为假  
其中正确的为（　　）
A、（1）（3）
B、（2）（3）
C、（1）（4）
D、（2）（4）
设奇函数f（x）定义在（-∞，0）∪（0，+∞）上，f（x）在（0，+∞）上为增函数，且f（1）=0，则不等式
3f(x)-2f(-x)
5x
＜0的解集为（　　）
A、（-1，0）∪（1，+∞）
B、（-∞，-1）∪（0，1）
C、（-∞，-1）∪（1，+∞）
D、（-1，0）∪（0，1）
已知l，m，n为互不重合的三条直线，平面α⊥平面β，α∩β=l，m?α，n?β，那么m⊥n是m⊥β的（　　）
A、充分不必要条件
B、必要不充分条件
C、充分必要条件
D、既不充分也不必要条件
时钟的时针和分针一天24小时内重合（　　）次．
A、21B、22C、23D、24
若函数y=x3-ax2+4在区间（0，2）内是单调递减函数，则实数a的取值范围是（　　）
A、a≥3B、a=3
C、a≤3D、0＜a＜3
给出下列命题：
①函数y=2-|x|为偶函数；
②函数y=1是周期函数；
③函数f（x）=2x-x2的零点有2个；
④函数g（x）=|log2x|-（
1
2
）x在（0，+∞）上恰有两个零点x1，x2且x1•x2＜1．
其中正确命题的个数是（　　）
A、1B、2C、3D、4
随机变量ξ的分布列如下：
ξ 0 1 2
P a b c
其中a，b，c成等差数列，则函数f（x）=x2+2x+ξ有且只有一个零点的概率为（　　）
A、
1
6
B、
1
3
C、
1
2
D、
5
6
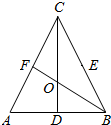在△ABC中，D、E、F分别是AB、BC、CA的中点，BF与CD交于点O，设向量
AB
=
a
，向量
AC
=
b
，
（1）证明A、O、E三点在同一条直线上，且
AO
OE
=
BO
OF
=
CO
OD
=2；
（2）用
a
，
b
表示
AO
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网