题目内容

15．已知函数F（x）=f（x）+x2是奇函数，且f（2）=1，则f（-2）=（　　）
A．9B．-9C．-7D．7

分析 根据函数y=f（x）+x2是奇函数，且f（2）=1，建立方程组，即可求f（-2）．

解答 解：∵F（x）=f（x）+x2是奇函数，∴F（-x）=-F（x），
即f（-x）+x2=-f（x）-x2，∴f（-x）+f（x）=-2x2，
即f（-2）+f（2）=-2×（-2）2=-8，
∴f（-2）=-f（2）-8=-9，
故选：B．

点评 本题主要考查函数奇偶性的应用，利用奇偶性的性质建立方程是解决本题的关键，属于基础题．

练习册系列答案
相关题目
5．设f（x）为奇函数，g（x）为偶函数，若f（x）+g（x）=x2-$\frac{1}{x}$，f（x）=-$\frac{1}{x}$．
6．若复数z=$\frac{-i}{1+2i}$（i是虚数单位），则z的实部为$-\frac{2}{5}$．
3．已知函数f（x）=（x-1）ex+$\frac{1}{2}a{x^2}+1$（其中a∈R）有两个零点，则a的取值范围是（-∞，-1）∪（-1，0）．
10．已知函数f（x）=$\frac{ln（2x）}{x}$，关于x的不等式f2（x）+af（x）＞0只有两个整数解，则实数a的取值范围是（　　）
A．$（-ln2，-\frac{1}{3}ln6]$B．$（-\frac{1}{e}，-\frac{ln6}{3}]$C．$[\frac{1}{3}ln6，ln2）$D．$[\frac{ln6}{3}，\frac{2}{e}）$
20．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的一个焦点与${y^2}=4\sqrt{3}x$的焦点重合，点$（\sqrt{3}，\frac{1}{2}）$在椭圆C上．
（1）求椭圆C的方程；
（2）设直线l：y=kx+m（k≠0）与椭圆交于P，Q两点，且以PQ为对角线的菱形的一顶点为（-1，0），若$|PQ|=\frac{{2\sqrt{6}}}{3}$，求k的值．
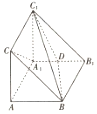7．如图，在直三棱柱ABC-A1B1C1中，D是A1B1的中点．
（1）求证：A1C∥平面BDC1；
（2）若AB⊥AC，且AB=AC=$\frac{2}{3}$AA1，求二面角A-BD-C1的余弦值．
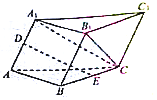4．如图，在三棱柱ABC-A1B1C1中，侧面ACC1A1⊥底面ABC，∠A1AC=60°，AC=2AA1=4，点D，E分别是AA1，BC的中点．
（1）证明：DE∥平面A1B1C；
（2）若AB=2，∠BAC=60°，求直线DE与平面ABB1A1所成角的正弦值．
5．若$a={log_{\frac{1}{π}}}\frac{1}{3}$，$b={e^{\frac{π}{3}}}$，$c={log_3}cos\frac{1}{5}π$，则（　　）
A．b＞c＞aB．b＞a＞cC．a＞b＞cD．c＞a＞b

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网