题目内容
设数列{an}的前n项和为Sn,a1=1,且Sn=n(Sn+1+an+1)(n∈N+).
(1)求Sn;
(2)若存在n≥2,使Sn-1λSn,Sn+1成等差数列,求正整数λ的值.
(1)求Sn;
(2)若存在n≥2,使Sn-1λSn,Sn+1成等差数列,求正整数λ的值.
考点:数列递推式,等差数列的性质
专题:等差数列与等比数列
分析:(1)由已知得Sn=n(Sn+1+Sn+1-Sn),从而
=
,由此利用累乘法能求出Sn=
.
(2)若存在n≥2,使Sn-1λSn,Sn+1成等差数列,则λ=
=
-
,由λ∈Z,推导出存在λ=1,此时n=3.
| Sn+1 |
| Sn |
| n+1 |
| 2n |
| n |
| 2n-1 |
(2)若存在n≥2,使Sn-1λSn,Sn+1成等差数列,则λ=
| 5n-3 |
| 4n |
| 5 |
| 4 |
| 3 |
| 4n |
解答:
解:(1)∵数列{an}的前n项和为Sn,a1=1,且Sn=n(Sn+1+an+1)(n∈N+),
∴S1=a1=1,Sn=n(Sn+1+Sn+1-Sn),
∴
=
,
∴Sn=S1×
×
×…×
=1×
×
×
×…×
=
.
∴Sn=
.
(2)若存在n≥2,使Sn-1λSn,Sn+1成等差数列,
则Sn-1+Sn+1=2λSn,即
+
=2λ•
,
∴λ=
=
-
,
∵n≥2,∴
≤λ<
,
∵λ∈Z,∴存在λ=1,此时n=3,
∴λ=1.
∴S1=a1=1,Sn=n(Sn+1+Sn+1-Sn),
∴
| Sn+1 |
| Sn |
| n+1 |
| 2n |
∴Sn=S1×
| S2 |
| S1 |
| S3 |
| S2 |
| Sn |
| Sn-1 |
=1×
| 2 |
| 2×1 |
| 3 |
| 2×2 |
| 4 |
| 2×3 |
| n |
| 2(n-1) |
=
| n |
| 2n-1 |
∴Sn=
| n |
| 2n-1 |
(2)若存在n≥2,使Sn-1λSn,Sn+1成等差数列,
则Sn-1+Sn+1=2λSn,即
| n-1 |
| 2n-2 |
| n+1 |
| 2n |
| n |
| 2n-1 |
∴λ=
| 5n-3 |
| 4n |
| 5 |
| 4 |
| 3 |
| 4n |
∵n≥2,∴
| 7 |
| 8 |
| 5 |
| 4 |
∵λ∈Z,∴存在λ=1,此时n=3,
∴λ=1.
点评:本题考查数列的前n项和的求法,考查满足条件的实数值的求法,解题时要认真审题,注意累乘法的合理运用.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
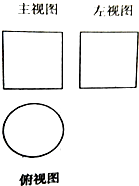 如图一个空间几何体的主视图和左视图都是边长为2的正方形,俯视图是一个圆,则该几何体的侧面积为
如图一个空间几何体的主视图和左视图都是边长为2的正方形,俯视图是一个圆,则该几何体的侧面积为