题目内容
已知各项均为正数的数列{an}满足:a2n+1=ta2n+(t-1)anan+1,其中n∈N*(1)若a2-a1=8,a3=a且数列{an}是唯一的.
①求a的值
②设数列{bn}满足bn=
,是否存在正整数m、n(1<m<n),使得b1、bm、bn成等比数列?若存在,求出所有的m、n的值;若不存在,请说明理由.
①求a的值
②设数列{bn}满足bn=
| nan |
| 4(2n+1)2n |
考点:数列递推式,等比数列的性质
专题:等差数列与等比数列
分析:①a2n+1=ta2n+(t-1)anan+1,因式分解为(an+1+an)(an+1-tan)=0,由于数列{an}是各项均为正数的数列,可得an+1=tan.数列{an}是等比数列,公比为t.
利用a2-a1=8,a3=a且数列{an}是唯一的.可得8t2-at+a=0,令△=0,(a≠0),即可解出.
②由①可得:an=a3•tn-3=2n+2.bn=
,假设存在正整数m、n(1<m<n),使得b1、bm、bn成等比数列,则
=b1•bn,即(
)2=
×
,解出即可.
利用a2-a1=8,a3=a且数列{an}是唯一的.可得8t2-at+a=0,令△=0,(a≠0),即可解出.
②由①可得:an=a3•tn-3=2n+2.bn=
| n |
| 2n+1 |
| b | 2 m |
| m |
| 2m+1 |
| 1 |
| 3 |
| n |
| 2n+1 |
解答:
解:①∵a2n+1=ta2n+(t-1)anan+1,∴(an+1+an)(an+1-tan)=0,
∵数列{an}是各项均为正数的数列,∴an+1+an>0,
∴an+1=tan.
∴数列{an}是等比数列,公比为t.
∵a2-a1=8,a3=a且数列{an}是唯一的.
∴ta1-a1=8,a=t2a1,
化为8t2-at+a=0,
令△=a2-32a=0,(a≠0),
解得a=32.此时t=2.
②由①可得:an=a3•tn-3=32×2n-3=2n+2.
∴bn=
=
,
假设存在正整数m、n(1<m<n),使得b1、bm、bn成等比数列,
则
=b1•bn,
∴(
)2=
×
,
化为6+
=(2+
)2,
当m=2时,解得n=12,满足题意,因此m=2,n=12.
当n≥3时,右边≤(2+
)2=
,∴6+
≤
,解得n<0,不符合题意,舍去.
因此存在唯一一对正整数m=2,n=12(1<m<n),使得b1、bm、bn成等比数列.
∵数列{an}是各项均为正数的数列,∴an+1+an>0,
∴an+1=tan.
∴数列{an}是等比数列,公比为t.
∵a2-a1=8,a3=a且数列{an}是唯一的.
∴ta1-a1=8,a=t2a1,
化为8t2-at+a=0,
令△=a2-32a=0,(a≠0),
解得a=32.此时t=2.
②由①可得:an=a3•tn-3=32×2n-3=2n+2.
∴bn=
| nan |
| 4(2n+1)2n |
| n |
| 2n+1 |
假设存在正整数m、n(1<m<n),使得b1、bm、bn成等比数列,
则
| b | 2 m |
∴(
| m |
| 2m+1 |
| 1 |
| 3 |
| n |
| 2n+1 |
化为6+
| 3 |
| n |
| 1 |
| m |
当m=2时,解得n=12,满足题意,因此m=2,n=12.
当n≥3时,右边≤(2+
| 1 |
| 3 |
| 49 |
| 9 |
| 3 |
| n |
| 49 |
| 9 |
因此存在唯一一对正整数m=2,n=12(1<m<n),使得b1、bm、bn成等比数列.
点评:本题考查了等比数列的定义及其通项公式、整数的性质,考查了分析问题与解决问题的能力,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
“m=4”是“直线mx+(1-m)y+1=0和直线3x+my-1=0垂直”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
若i为虚数单位,则i+i2+i3+i4的值为( )
| A、-1 | B、i | C、0 | D、1 |
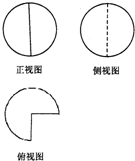 一个半径为1的球体经过切割后,剩余部分几何体的三视图如图所示,则该几何体的表面积为( )
一个半径为1的球体经过切割后,剩余部分几何体的三视图如图所示,则该几何体的表面积为( )| A、16π | ||
| B、14π | ||
| C、4π | ||
D、
|