��Ŀ����
��֪�ȱ�����{an}��ǰn���ΪSn����S10��S5=1��2���ֶ��κ���y=
x2+
x+5�ĵ���������һϵ�е�P1��x1��y1����P2��x2��y2��������Pn��xn��yn��������n��1��n��N���ҵ�Pn�ĺ����깹�ɵȲ�����{xn}����x3=-
��x5=-
��
��1������κ�������ʽ����Pn�����ꣻ
��2������������C1��C2��C3������Cn�����е�ÿһ���ĶԳ��ᶼ��ֱ��x�ᣬ������Cn�Ķ���ΪPn���ҹ���Dn��0��n2+1��������������Cn�����ڵ�Dn��ֱ�ߵ�б��Ϊkn����֤��
+
+��+
��
��
��3����S={x|x=2xn��n��N*}��T={y|y=4yn��n��N*}���Ȳ�����{an}����һ��an����S��T������a1��S��T�е��������-265��a10��-125��������{an}��ͨ�ʽ��
| S15 |
| S10 |
| 13 |
| 4 |
| 9 |
| 2 |
| 13 |
| 2 |
��1������κ�������ʽ����Pn�����ꣻ
��2������������C1��C2��C3������Cn�����е�ÿһ���ĶԳ��ᶼ��ֱ��x�ᣬ������Cn�Ķ���ΪPn���ҹ���Dn��0��n2+1��������������Cn�����ڵ�Dn��ֱ�ߵ�б��Ϊkn����֤��
| 1 |
| k1k2 |
| 1 |
| k2k3 |
| 1 |
| kn-1kn |
| 1 |
| 10 |
��3����S={x|x=2xn��n��N*}��T={y|y=4yn��n��N*}���Ȳ�����{an}����һ��an����S��T������a1��S��T�е��������-265��a10��-125��������{an}��ͨ�ʽ��
���㣺������������ε��ۺ�
ר�⣺�����ĸ��Ӧ��,�Ȳ�������ȱ�����,����
��������1�����õȱ����е����ʽ���q5=-
���ٴ�����κ���ʽ������ɵý���ʽ�����y�ĵ��������õȲ����е�ͨ����ɵõ�xn�������õ���yn��
��2�����ô���ϵ�������������Cn�Ľ���ʽ�����������õ����ߵ�б�ʣ���������������ͣ����ɵ�֤��
��3���������S��T����ý��������������������е�������ɵȲ����е�ͨ�ʽ�����ɵõ���
| 1 |
| 2 |
��2�����ô���ϵ�������������Cn�Ľ���ʽ�����������õ����ߵ�б�ʣ���������������ͣ����ɵ�֤��
��3���������S��T����ý��������������������е�������ɵȲ����е�ͨ�ʽ�����ɵõ���
���
��1���⣺�ȱ�����{an}��ǰn���ΪSn����S10��S5=1��2��
��Ȼ���Ȳ�Ϊ1����
��
=1��2��
�����1+q5=
����q5=-
����
=
=
=
��
���ж��κ���y=
x2+
x+5��y��=3x+
��
�Ȳ�����{xn}����x3=-
��x5=-
����d=
=-1��
��xn=-
-��n-3��=-n-
��
����yn=3��-n-
��+
=-3n-
��
����κ�������ʽy=
x2+
x+5����Pn��������-n-
��-3n-
����
��2��֤������������Cn��y-yn=a��x-xn��2��
�ɣ�1���ɵ�y+3n+
=a��x+n+
��2��
��x=0����y=a��n+
��2-3n-
=n2+1��
���a=1������y=��x+n+
��2-��3n+
����
y��=2��x+n+
��������kn=2n+3��
��
=
=
��
-
����
����
+
+��+
=
����
-
+
-
+��+
-
��
=
����
-
����
��
��3���⣺S={x|x=2xn=-2n-3��n��N*}��T={y|y=4yn=-12n-5��n��N*}��
�ɵ�S��T=T��T������Ϊ-17��
�Ȳ�����{an}����һ��an��S��T������a1��S��T�е��������
��dΪ-12��������������a1=-17��
��-265��a10��-125���ɵ�-265��-17+9d��-125��
���-
��d��-12���ɵ�d=-24��
����an=-17+��n-1��•��-24��=-24n+7��
��Ȼ���Ȳ�Ϊ1����
| a1(1-q10) |
| 1-q |
| a1(1-q5) |
| 1-q |
�����1+q5=
| 1 |
| 2 |
| 1 |
| 2 |
| S15 |
| S10 |
| 1-q15 |
| 1-q10 |
1+
| ||
1-
|
| 3 |
| 2 |
���ж��κ���y=
| 3 |
| 2 |
| 13 |
| 4 |
| 13 |
| 4 |
�Ȳ�����{xn}����x3=-
| 9 |
| 2 |
| 13 |
| 2 |
| x5-x3 |
| 5-3 |
��xn=-
| 9 |
| 2 |
| 3 |
| 2 |
����yn=3��-n-
| 3 |
| 2 |
| 13 |
| 4 |
| 5 |
| 4 |
����κ�������ʽy=
| 3 |
| 2 |
| 13 |
| 4 |
| 3 |
| 2 |
| 5 |
| 4 |
��2��֤������������Cn��y-yn=a��x-xn��2��
�ɣ�1���ɵ�y+3n+
| 5 |
| 4 |
| 3 |
| 2 |
��x=0����y=a��n+
| 3 |
| 2 |
| 5 |
| 4 |
���a=1������y=��x+n+
| 3 |
| 2 |
| 5 |
| 4 |
y��=2��x+n+
| 3 |
| 2 |
��
| 1 |
| kn-1kn |
| 1 |
| (2n+1)(2n+3) |
| 1 |
| 2 |
| 1 |
| 2n+1 |
| 1 |
| 2n+3 |
����
| 1 |
| k1k2 |
| 1 |
| k2k3 |
| 1 |
| kn-1kn |
| 1 |
| 2 |
| 1 |
| 5 |
| 1 |
| 7 |
| 1 |
| 7 |
| 1 |
| 9 |
| 1 |
| 2n+1 |
| 1 |
| 2n+3 |
=
| 1 |
| 2 |
| 1 |
| 5 |
| 1 |
| 2n+3 |
| 1 |
| 10 |
��3���⣺S={x|x=2xn=-2n-3��n��N*}��T={y|y=4yn=-12n-5��n��N*}��
�ɵ�S��T=T��T������Ϊ-17��
�Ȳ�����{an}����һ��an��S��T������a1��S��T�е��������
��dΪ-12��������������a1=-17��
��-265��a10��-125���ɵ�-265��-17+9d��-125��
���-
| 248 |
| 9 |
����an=-17+��n-1��•��-24��=-24n+7��
���������⿼��Ȳ����к͵ȱ����е�ͨ������ʽ�����ã��������е���ͷ���������������ͣ����鵼���ļ������壺�����ڸõ㴦���ߵ�б�ʣ��������������������е�����״��⣮

��ϰ��ϵ�д�
 ��Ȥ����¹�֪��ϵ�д�
��Ȥ����¹�֪��ϵ�д� Ӣ��СӢ������Ĭдϵ�д�
Ӣ��СӢ������Ĭдϵ�д� �����ҵ���������ͯ������ϵ�д�
�����ҵ���������ͯ������ϵ�д�
�����Ŀ
��֪a��b��c�ֱ�Ϊ��ABC�������ڽ�A��B��C�ĶԱߣ���a=2
��b=2
��A=60�㣬���B���ڣ�������
| 3 |
| 2 |
| A��45���135�� | B��135�� |
| C��60�� | D��45�� |
��cos2��=-
���ǡ���=k��+
��k��Z���ģ�������
| ||
| 2 |
| 5�� |
| 12 |
| A����ֲ���Ҫ���� |
| B����Ҫ��������� |
| C����Ҫ���� |
| D���Ȳ����Ҳ����Ҫ���� |
��iΪ������λ����i+i2+i3+i4��ֵΪ��������
| A��-1 | B��i | C��0 | D��1 |
��֪����A={-2��0��1}��B={0��1��2}����A��B���ڣ�������
| A��{0��1} |
| B��{-2��0��1} |
| C��{-2��0��1��2} |
| D��{-2��2} |
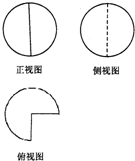 һ���뾶Ϊ1�����徭���и��ʣ�ಿ�ּ����������ͼ��ͼ��ʾ����ü�����ı����Ϊ��������
һ���뾶Ϊ1�����徭���и��ʣ�ಿ�ּ����������ͼ��ͼ��ʾ����ü�����ı����Ϊ��������| A��16�� | ||
| B��14�� | ||
| C��4�� | ||
D��
|