题目内容
(1)先后抛掷一枚硬币四次,求两次正面朝上的概率;
(2)在区间(0,3)中随机地取出两个数a、b,求点(a,b)在圆x2+y2=4内的概率.
(2)在区间(0,3)中随机地取出两个数a、b,求点(a,b)在圆x2+y2=4内的概率.
考点:几何概型,列举法计算基本事件数及事件发生的概率
专题:计算题,概率与统计
分析:(1)确定基本事件总数为16,两次正面朝上总数为
=6,即可求两次正面朝上的概率;
(2)求出在区间(0,3)中随机地取出两个数a、b,区域面积为3×3=9,点(a,b)在圆x2+y2=4内的面积,即可求出概率.
| C | 2 4 |
(2)求出在区间(0,3)中随机地取出两个数a、b,区域面积为3×3=9,点(a,b)在圆x2+y2=4内的面积,即可求出概率.
解答:
 解:(1)基本事件总数为16,两次正面朝上总数为
解:(1)基本事件总数为16,两次正面朝上总数为
=6,
∴两次正面朝上的概率为
=
;
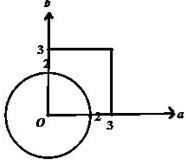
(2)如图所示,在区间(0,3)中随机地取出两个数a、b,区域面积为3×3=9,
点(a,b)在圆x2+y2=4内的面积为
π×22=π,
∴点(a,b)在圆x2+y2=4内的概率
.
 解:(1)基本事件总数为16,两次正面朝上总数为
解:(1)基本事件总数为16,两次正面朝上总数为| C | 2 4 |
∴两次正面朝上的概率为
| 6 |
| 16 |
| 3 |
| 8 |
(2)如图所示,在区间(0,3)中随机地取出两个数a、b,区域面积为3×3=9,
点(a,b)在圆x2+y2=4内的面积为
| 1 |
| 4 |
∴点(a,b)在圆x2+y2=4内的概率
| π |
| 9 |
点评:本题考查等可能事件的概率,考查几何概型,解题的关键是确定其测度.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
 执行如图所示的程序框图,若输入数据n=5,a1=-2,a2=-2.6,a3=3.2,a4=2.5,a5=1.4,则输出的结果为( )
执行如图所示的程序框图,若输入数据n=5,a1=-2,a2=-2.6,a3=3.2,a4=2.5,a5=1.4,则输出的结果为( )| A、0.3 | B、0.4 |
| C、0.5 | D、0.6 |
 如图甲,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD,E、F、G分别是PC、PD、BC的中点,现将△PDC沿CD折起,使平面PDC⊥平面ABCD(如图乙),且所得到的四棱锥P-ABCD的正视图、侧视图、俯视图的面积总和为8.
如图甲,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD,E、F、G分别是PC、PD、BC的中点,现将△PDC沿CD折起,使平面PDC⊥平面ABCD(如图乙),且所得到的四棱锥P-ABCD的正视图、侧视图、俯视图的面积总和为8.