题目内容
在一个口袋内装有7个相同的球,其中三个球标有数字0,4个球标有数字1,若从袋中摸出3个球,那么摸出的三个球所标数字之和小于2或大于3的概率是多少?
考点:古典概型及其概率计算公式
专题:概率与统计
分析:将“摸出的五个球所标数字之和小于2或大于3”记为事件A,其对立事件
,由题意求得P(
),进而根据对立事件概率减法公式,得到答案.
. |
| A |
. |
| A |
解答:
解:从装有7个相同的球的袋中摸出3个球,共有
=35种情况,
将“摸出的五个球所标数字之和小于2或大于3”记为事件A,
则“摸出的五个球所标数字之和等于2或等于3”为事件
,
则
共包含
+
=18+4=22种情况,
故P(
)=
,
故P(A)=1-P(
)=
| C | 3 7 |
将“摸出的五个球所标数字之和小于2或大于3”记为事件A,
则“摸出的五个球所标数字之和等于2或等于3”为事件
. |
| A |
则
. |
| A |
| C | 2 4 |
| C | 1 3 |
| C | 3 4 |
故P(
. |
| A |
| 22 |
| 35 |
故P(A)=1-P(
. |
| A |
| 13 |
| 35 |
点评:本题考查的知识点是古典概型概率计算公式,其中熟练掌握利用古典概型概率计算公式求概率的步骤,是解答的关键.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
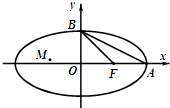 如图,椭圆C:
如图,椭圆C: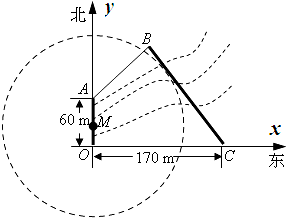 如图:为了保护河上古桥OA,规划建一座新桥BC,同时设立一个圆形保护区.经测量,点A位于点O正北方向60m处,点C位于点O正东方向170m处(OC为河岸).规划要求:新桥BC与河岸AB垂直,保护区的边界为圆心M(在线段OA上)与BC相切的圆.建立如图所示的直角坐标系,已知新桥BC所在直线的方程为:4x+3y-680=0.
如图:为了保护河上古桥OA,规划建一座新桥BC,同时设立一个圆形保护区.经测量,点A位于点O正北方向60m处,点C位于点O正东方向170m处(OC为河岸).规划要求:新桥BC与河岸AB垂直,保护区的边界为圆心M(在线段OA上)与BC相切的圆.建立如图所示的直角坐标系,已知新桥BC所在直线的方程为:4x+3y-680=0.