题目内容
若等差数列{an}的前n项和为Sn,且满足
为常数,则称该数列为“优”数列.
(1)判断an=4n-2是否为“优”数列?并说明理由;
(2)若首项为1,且公差不为零的等差数列{an}为“优”数列,试求出该数列的通项公式;
(3)若首项为1,且公差不为零的等差数列{an}为“优”数列,正整数k,h满足k+h=2013,求
+
的最小值.
| Sn |
| S2n |
(1)判断an=4n-2是否为“优”数列?并说明理由;
(2)若首项为1,且公差不为零的等差数列{an}为“优”数列,试求出该数列的通项公式;
(3)若首项为1,且公差不为零的等差数列{an}为“优”数列,正整数k,h满足k+h=2013,求
| 4 | ||
|
| 1 | ||
|
考点:数列的应用
专题:综合题,等差数列与等比数列
分析:(1)利用“优”数列,代入验证即可;
(2)由
=k,首项为1,可得2n+n2d-nd=4kn+4n2dk-2nkd,化简得d(4k-1)n+(2k-1)(2-d)=0,从而可得
,即可得出结论;
(3)
+
=
+
=
(k+h)(
+
),利用基本不等式,即可得出结论.
(2)由
| Sn |
| S2n |
|
(3)
| 4 | ||
|
| 1 | ||
|
| 4 |
| k |
| 1 |
| h |
| 1 |
| 2013 |
| 4 |
| k |
| 1 |
| h |
解答:
解:(1)由an=4n-2,得a1=2,d=4,
∴
=
=
,
∴an=4n-2是“优”数列;
(2)设等差数列{an},公差为d,则由
=k,首项为1,可得2n+n2d-nd=4kn+4n2dk-2nkd,
化简得d(4k-1)n+(2k-1)(2-d)=0①,
由于①对任意正整数n均成立,∴
,
∴d=2,k=
,
∴an=2n-1;
(3)由(2)知an=2n-1,正整数k,h满足k+h=2013,
∴
+
=
+
=
(k+h)(
+
)=
(5+
+
)≥
(5+4)=
,
当且仅当k=2h=1342时,
+
的最小值为
.
∴
| Sn |
| S2n |
| ||
|
| 1 |
| 4 |
∴an=4n-2是“优”数列;
(2)设等差数列{an},公差为d,则由
| Sn |
| S2n |
化简得d(4k-1)n+(2k-1)(2-d)=0①,
由于①对任意正整数n均成立,∴
|
∴d=2,k=
| 1 |
| 4 |
∴an=2n-1;
(3)由(2)知an=2n-1,正整数k,h满足k+h=2013,
∴
| 4 | ||
|
| 1 | ||
|
| 4 |
| k |
| 1 |
| h |
| 1 |
| 2013 |
| 4 |
| k |
| 1 |
| h |
| 1 |
| 2013 |
| k |
| h |
| 4h |
| k |
| 1 |
| 2013 |
| 3 |
| 671 |
当且仅当k=2h=1342时,
| 4 | ||
|
| 1 | ||
|
| 3 |
| 671 |
点评:本题考查新定义,考查等差数列的求和公式,考查基本不等式的运用,综合性强.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
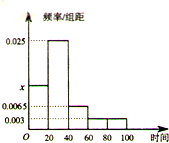 某学校随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100).
某学校随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100).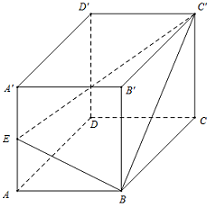 已知正方体ABCD-A′B′C′D′中,E是AA′棱的中点.求平面BEC′与平面ABCD所成的角的余弦值.
已知正方体ABCD-A′B′C′D′中,E是AA′棱的中点.求平面BEC′与平面ABCD所成的角的余弦值. 在△ABC中,已知
在△ABC中,已知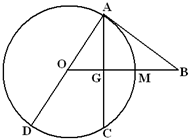 如图,已知AD为圆O的直径,直线BA与圆O相切于点A,直线OB与弦AC垂直并相交于点G,与弧AC相交于M,连接DC,AB=10,AC=12.
如图,已知AD为圆O的直径,直线BA与圆O相切于点A,直线OB与弦AC垂直并相交于点G,与弧AC相交于M,连接DC,AB=10,AC=12. 如图,已知BC为⊙O的直径,点A、F在⊙O上,AD⊥BC,垂足为D,BF交AD于E,且AE=BE.
如图,已知BC为⊙O的直径,点A、F在⊙O上,AD⊥BC,垂足为D,BF交AD于E,且AE=BE.