题目内容
已知函数y=-x3-3x+5零点所在区间为（ ）
| A、（0，1） |
| B、（1，2） |
| C、（-1，0） |
| D、（2，3） |
考点：二分法求方程的近似解
专题：计算题,函数的性质及应用
分析：易知函数y=-x3-3x+5在R上连续且单调递减，从而由函数的零点的判定定理判断即可．
解答：
解：易知函数y=-x3-3x+5在R上连续且单调递减，
f（1）=-1-3+5=1＞0，f（2）=-8-6+5=-9＜0；
故f（1）•f（2）＜0，
故函数f（x）=-x3-3x+5的零点所在的区间为（1，2）；
故选：B．
f（1）=-1-3+5=1＞0，f（2）=-8-6+5=-9＜0；
故f（1）•f（2）＜0，
故函数f（x）=-x3-3x+5的零点所在的区间为（1，2）；
故选：B．
点评：本题考查了函数的零点的判定定理的应用，属于基础题．
练习册系列答案
文敬图书课时先锋系列答案
相关题目
若集合A={x|x2-2x-16≤0}，B={x|C5x≤5}，则A∩B中元素个数为]（ ）
| A、4个 | B、6个 | C、2个 | D、0个 |
如图，在平行四边形ABCD中，点E在边CD上，若在平行四边形ABCD内部随机取一个点Q，则点Q取自△ABE内部的概率是
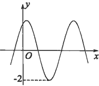如图，函数f（x）=Asin（2x+φ）（A＞0，|φ|＜| π |
| 2 |
| 3 |
A、（-
| ||
B、（-
| ||
C、（
| ||
D、（
|