题目内容
14.由曲线y=$\sqrt{x}$,y=x-2及x轴所围成的封闭图形的面积是( )| A. | 4 | B. | $\frac{10}{3}$ | C. | $\frac{16}{3}$ | D. | $\frac{15}{4}$ |
分析 根据定积分的几何意义,先求出积分的上下限,即可求出所围成的图形的面积
解答  解:联立直线y=x-2,曲线y=$\sqrt{x}$构成方程组,解得$\left\{\begin{array}{l}{x=4}\\{y=2}\end{array}\right.$,
解:联立直线y=x-2,曲线y=$\sqrt{x}$构成方程组,解得$\left\{\begin{array}{l}{x=4}\\{y=2}\end{array}\right.$,
联立直线y=x-2,y=0构成方程组,解得$\left\{\begin{array}{l}{x=2}\\{y=0}\end{array}\right.$
∴曲线y=$\sqrt{x}$,y=x-2及x轴所围成的封闭图形的面积
S=${∫}_{0}^{4}$$\sqrt{x}$dx-${∫}_{2}^{4}$(x-2)dx=$\frac{2}{3}{x}^{\frac{3}{2}}$|${\;}_{0}^{4}$-($\frac{1}{2}{x}^{2}-2x$)|${\;}_{2}^{4}$=$\frac{16}{3}$-2=$\frac{10}{3}$.
故选:B.
点评 本题考查了定积分的几何意义,关键是求出积分的上下限,属于基础题.

练习册系列答案
相关题目
9.已知集合A={x|-1≤x≤1},B={x|x2-5x+6≥0},则下列结论中正确的是( )
| A. | A∩B=B | B. | A∪B=A | C. | A?B | D. | ∁RA=B |
4.已知函数$f(x)=\left\{\begin{array}{l}{log_2}x,x>0\\ sin\frac{π}{6}x,x≤0\end{array}\right.$,则$f[{f(\frac{1}{4})}]$=( )
| A. | $\frac{1}{2}$ | B. | -1 | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
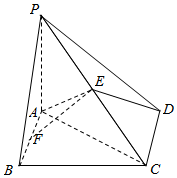 如图,在四棱锥中P-ABCD,底面ABCD为边长为$\sqrt{2}$的正方形,PA⊥BD.
如图,在四棱锥中P-ABCD,底面ABCD为边长为$\sqrt{2}$的正方形,PA⊥BD.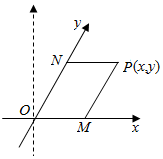 如图,将平面直角坐标系中的纵轴绕原点O顺时针旋转30°后,构成一个斜坐标平面xOy.在此斜坐标平面xOy中,点P(x,y)的坐标定义如下:过点P作两坐标轴的平行线,分别交两轴于M,N两点,则M在Ox轴上表示的数为x,N在Oy轴上表示的数为y.那么以原点O为圆心的单位圆在此斜坐标系下的方程为x2+y2+xy-1=0.
如图,将平面直角坐标系中的纵轴绕原点O顺时针旋转30°后,构成一个斜坐标平面xOy.在此斜坐标平面xOy中,点P(x,y)的坐标定义如下:过点P作两坐标轴的平行线,分别交两轴于M,N两点,则M在Ox轴上表示的数为x,N在Oy轴上表示的数为y.那么以原点O为圆心的单位圆在此斜坐标系下的方程为x2+y2+xy-1=0. 如图,在四棱锥S-ABCD中,侧棱SA⊥底面ABCD,且底面ABCD是边长为1的正方形,侧棱SA=4,AC与BD相交于点O.
如图,在四棱锥S-ABCD中,侧棱SA⊥底面ABCD,且底面ABCD是边长为1的正方形,侧棱SA=4,AC与BD相交于点O.