题目内容
4.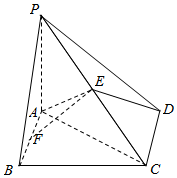 如图,在四棱锥中P-ABCD,底面ABCD为边长为$\sqrt{2}$的正方形,PA⊥BD.
如图,在四棱锥中P-ABCD,底面ABCD为边长为$\sqrt{2}$的正方形,PA⊥BD.(Ⅰ)求证:PB=PD;
(Ⅱ)若E,F分别为PC,AB的中点,EF⊥平面PCD,求三棱锥的D-ACE体积.
分析 (I)由正方形的性质得AC⊥BD,又BD⊥PA,故BD⊥平面PAC,于是BD⊥PO,由Rt△PBO∽Rt△PDO得出PB=PD;
(II)取PD的中点Q,连接AQ,EQ,则可证四边形AFEQ是平行四边形,故EF∥AQ,于是AQ⊥平面PCD,得出AQ⊥PD,于是PA=AD=$\sqrt{2}$,由CD⊥AD,CD⊥AQ得CD⊥平面PAD,故CD⊥PA,于是PA⊥平面ABCD,则E到底面的距离等于$\frac{1}{2}PA$,代入棱锥的体积公式计算.
解答 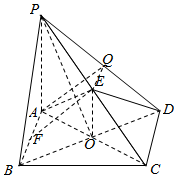 解:(Ⅰ)连接AC交BD于点O,
解:(Ⅰ)连接AC交BD于点O,
∵底面ABCD是正方形,
∴AC⊥BD且O为BD的中点.
又PA⊥BD,PA∩AC=A,
∴BD⊥平面PAC,又PO?平面PAC,
∴BD⊥PO.又BO=DO,
∴Rt△PBO∽Rt△PDO,
∴PB=PD.
(Ⅱ)取PD的中点Q,连接AQ,EQ,则EQ$\stackrel{∥}{=}$$\frac{1}{2}$CD,
又AF$\stackrel{∥}{=}\frac{1}{2}CD$,
∴AFEQ为平行四边形,EF∥AQ,
∵EF⊥平面PCD,
∴AQ⊥平面PCD,∵PD?平面PCD,
∴AQ⊥PD,∵Q是PD的中点,
∴AP=AD=$\sqrt{2}$.
∵AQ⊥平面PCD,CD?平面PCD,
∴AQ⊥CD,又AD⊥CD,又AQ∩AD=A,
∴CD⊥平面PAD
∴CD⊥PA,又BD⊥PA,CD∩BD=D,
∴PA⊥平面ABCD.
$\begin{array}{l}{V_{D-ACE}}={V_{E-ACD}}\\=\frac{1}{3}×\frac{1}{2}PA×{S_{△ACD}}\end{array}$
$\begin{array}{l}=\frac{1}{3}×\frac{1}{2}×\sqrt{2}×\frac{1}{2}×\sqrt{2}×\sqrt{2}\\=\frac{{\sqrt{2}}}{6}\end{array}$
故三棱锥D-ACE的体积为$\frac{{\sqrt{2}}}{6}$.
点评 本题考查了线面垂直的判定与性质,棱锥的体积计算,属于中档题.

 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案| A. | 4 | B. | $\frac{10}{3}$ | C. | $\frac{16}{3}$ | D. | $\frac{15}{4}$ |
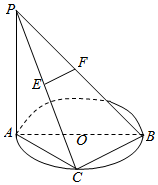 如图,已知PA垂直圆O所在的平面,AB是圆O的直径,AB=2,C是圆O上一点,且PA=AC=BC,E,F分别为PC,PB中点.
如图,已知PA垂直圆O所在的平面,AB是圆O的直径,AB=2,C是圆O上一点,且PA=AC=BC,E,F分别为PC,PB中点.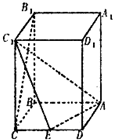 已知四棱柱ABCD-A1B1C1D1,底面ABCD为菱形,∠ADC=60°,BB1⊥底面ABCD,AA1=AC=4,E是CD的中点,
已知四棱柱ABCD-A1B1C1D1,底面ABCD为菱形,∠ADC=60°,BB1⊥底面ABCD,AA1=AC=4,E是CD的中点,