题目内容
19. 如图,在四棱锥S-ABCD中,侧棱SA⊥底面ABCD,且底面ABCD是边长为1的正方形,侧棱SA=4,AC与BD相交于点O.
如图,在四棱锥S-ABCD中,侧棱SA⊥底面ABCD,且底面ABCD是边长为1的正方形,侧棱SA=4,AC与BD相交于点O.(1)证明:SO⊥BD;
(2)求三棱锥O-SCD的体积.
分析 (1)由SA⊥平面ABCD可得SA⊥BD,又AC⊥BD,故BD⊥平面SAC,于是BD⊥SO;
(2)VO-SCD=VS-OCD=$\frac{1}{3}{S}_{△OCD}•SA$.
解答 证明:(1)∵SA⊥平面ABCD,BD?平面ABCD,
∴SA⊥BD,
∵四边形ABCD是正方形,
∴BD⊥AC,
又SA?平面SAC,AC?平面SAC,SA∩AC=A,
∴BD⊥平面SAC,∵SO?平面SAC,
∴SO⊥BD.
(2)∵四边形ABCD是边长为1的正方形,
∴S△OCD=$\frac{1}{4}$S正方形ABCD=$\frac{1}{4}×{1}^{2}$=$\frac{1}{4}$.
∴VO-SCD=VS-OCD=$\frac{1}{3}{S}_{△OCD}•SA$=$\frac{1}{3}×\frac{1}{4}×4$=$\frac{1}{3}$.
点评 本题考查了线面垂直的判定与性质,棱锥的体积计算,属于基础题.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
14.由曲线y=$\sqrt{x}$,y=x-2及x轴所围成的封闭图形的面积是( )
| A. | 4 | B. | $\frac{10}{3}$ | C. | $\frac{16}{3}$ | D. | $\frac{15}{4}$ |
8.如果a<b<0,那么下面一定成立的是( )
| A. | ac<bc | B. | a-b>0 | C. | a2>b2 | D. | $\frac{1}{a}$<$\frac{1}{b}$ |
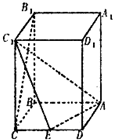 已知四棱柱ABCD-A1B1C1D1,底面ABCD为菱形,∠ADC=60°,BB1⊥底面ABCD,AA1=AC=4,E是CD的中点,
已知四棱柱ABCD-A1B1C1D1,底面ABCD为菱形,∠ADC=60°,BB1⊥底面ABCD,AA1=AC=4,E是CD的中点,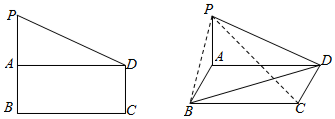 如图,在直角梯形PBCD中,PB∥DC,DC⊥BC,PB=BC=2CD=2,点A是PB的中点,现沿AD将平面PAD折起,设∠PAB=θ:
如图,在直角梯形PBCD中,PB∥DC,DC⊥BC,PB=BC=2CD=2,点A是PB的中点,现沿AD将平面PAD折起,设∠PAB=θ:
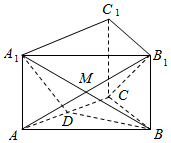 如图,三棱柱ABC-A1B1C1中,A1A⊥平面ABC,△ABC是边长为2的正三角形,D是AC的中点.
如图,三棱柱ABC-A1B1C1中,A1A⊥平面ABC,△ABC是边长为2的正三角形,D是AC的中点.