题目内容
若命题“?x0∈R，使得
+mx0+2m-3＜0”为假命题，则实数m的取值范围是 ．．
| x | 2 0 |
考点：特称命题,复合命题的真假
专题：不等式的解法及应用
分析：由于命题P：“?x0∈R，使得
+mx0+2m-3＜0”为假命题，可得￢P：“?x∈R，x2+mx+2m-3≥0”为真命题，因此△≤0，解出即可．
| x | 2 0 |
解答：
解：∵命题P：“?x0∈R，使得
+mx0+2m-3＜0”为假命题，
∴￢P：“?x∈R，x2+mx+2m-3≥0”为真命题，∴△≤0，即m2-4（2m-3）≤0，解得2≤m≤6．
∴实数m的取值范围是[2，6]．
故答案为：[2，6]．
| x | 2 0 |
∴￢P：“?x∈R，x2+mx+2m-3≥0”为真命题，∴△≤0，即m2-4（2m-3）≤0，解得2≤m≤6．
∴实数m的取值范围是[2，6]．
故答案为：[2，6]．
点评：本题考查了非命题、一元二次不等式恒成立与判别式的关系，属于基础题．
练习册系列答案
相关题目
设等比数列{an}的前n项和为Sn，若Sm-1=5，Sm=-11，Sm+1=21，则m=（ ）
| A、3 | B、4 | C、5 | D、6 |
已知a、b都是实数，a≠0，f（x）=|x-1|+|x-2|．
（1）若f（x）＞2，求实数x的取值范围；
（2）若|a+b|+|a-b|≥|a|f（x）对满足条件的所有a、b都成立，求实数x的取值范围．
（1）若f（x）＞2，求实数x的取值范围；
（2）若|a+b|+|a-b|≥|a|f（x）对满足条件的所有a、b都成立，求实数x的取值范围．
已知a＞1，b＞1，且lnalnb=
，则ab（ ）
| 1 |
| 4 |
| A、有最大值1 |
| B、有最小值1 |
| C、有最大值e |
| D、有最小值e |
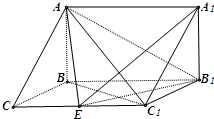如图，在三棱柱ABC-A1B1C1中，已知BC=1，BB1=2，∠BCC1=90°，AB⊥侧面BB1C1C．