题目内容
设数列{an}的前n项和为Sn,且a1=1,an+1=2Sn(n=1,2,3…),给出下列四个命题:
①数列{an}是等比数列;
②数列{Sn}是等比数列;
③?常数c>0,使
≤c(n∈N+)恒成立;
④若Sn(3an-2γ)+2≥0(n=1,2,3…)恒成立,则γ∈(+∞,
).
以上命题中正确的命题是 (写出所有正确命题的序号).
①数列{an}是等比数列;
②数列{Sn}是等比数列;
③?常数c>0,使
| n |
 |
| i=1 |
| 1 |
| ai |
④若Sn(3an-2γ)+2≥0(n=1,2,3…)恒成立,则γ∈(+∞,
| 10 |
| 3 |
以上命题中正确的命题是
考点:数列递推式
专题:等差数列与等比数列
分析:①求出数列{an}的通项公式,根据等比数列的定义进行判断.
②求出数列{Sn}的通项公式,根据等比数列的定义进行判断.
③求出
≤c(n∈N+)的数值,根据不等式的性质进行判断.
④将Sn(3an-2γ)+2≥0(n=1,2,3…)恒成立,利用参数分离法求γ的取值范围即可进行判断.
②求出数列{Sn}的通项公式,根据等比数列的定义进行判断.
③求出
| n |
 |
| i=1 |
| 1 |
| ai |
④将Sn(3an-2γ)+2≥0(n=1,2,3…)恒成立,利用参数分离法求γ的取值范围即可进行判断.
解答:
解:①∵a1=1,an+1=2Sn,
∴an+2=2Sn+1,
两式相减得an+2-an+1=2Sn+1-2Sn=2an+1,
即an+2=3an+1,
即
=3,(n≥2),
当n=1时,a2=2a1=2,
=2≠3,
∴数列{an}不是等比数列;∴①错误.
②an+1=2Sn=Sn+1-Sn,
即3Sn=Sn+1,
∴
=3,(n≥1),
即数列{Sn}是等比数列;∴②正确.
③由①知,当n≥2时,an=a23n-2=2•3n-2,a1=1,
则
=
•(
)n-2,n≥2,
=1,
则
=
+
=1+
-
(
)n-2<
,
∴当c≥
时,使
≤c(n∈N+)恒成立;∴③正确.
④由Sn(3an-2γ)+2≥0得3Snan-2γSn+2≥0,
即γ≤
(n=1,2,3…)恒成立,
当n=1时,γ≤
=
,
当n≥2时,γ≤
=
an+
=
an+
=
×2?3n-2+
=3n-1+
≥2
=2,
当且仅当3n-1=
,即3n-1=1,n=1取等号,此时不成立.
设t=3n-1,当n≥2时,t≥3,
∵y=3n-1+
=t+
在[3,+∞)上单调递增,
∴y≥3+
=
,
∴要使γ≤
(n=1,2,3…)恒成立,
则γ≤
,
即γ∈(-∞,
],∴④错误.
故正确的是②③,
故答案为:②③.
∴an+2=2Sn+1,
两式相减得an+2-an+1=2Sn+1-2Sn=2an+1,
即an+2=3an+1,
即
| an+2 |
| an+1 |
当n=1时,a2=2a1=2,
| a2 |
| a1 |
∴数列{an}不是等比数列;∴①错误.
②an+1=2Sn=Sn+1-Sn,
即3Sn=Sn+1,
∴
| Sn+1 |
| Sn |
即数列{Sn}是等比数列;∴②正确.
③由①知,当n≥2时,an=a23n-2=2•3n-2,a1=1,
则
| 1 |
| an |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| a1 |
则
| n |
 |
| i=1 |
| 1 |
| ai |
| 1 |
| a1 |
| ||||
1-
|
| 3 |
| 4 |
| 3 |
| 4 |
| 1 |
| 3 |
| 7 |
| 4 |
∴当c≥
| 7 |
| 4 |
| n |
 |
| i=1 |
| 1 |
| ai |
④由Sn(3an-2γ)+2≥0得3Snan-2γSn+2≥0,
即γ≤
| 3Snan+2 |
| 2Sn |
当n=1时,γ≤
| 3a1a1+2 |
| 2a1 |
| 5 |
| 2 |
当n≥2时,γ≤
| 3Snan+2 |
| 2Sn |
| 3 |
| 2 |
| 1 |
| Sn |
| 3 |
| 2 |
| 2 |
| an+1 |
| 3 |
| 2 |
| 2 |
| 2?3n-1 |
| 1 |
| 3n-1 |
3n-1?
|
当且仅当3n-1=
| 1 |
| 3n-1 |
设t=3n-1,当n≥2时,t≥3,
∵y=3n-1+
| 1 |
| 3n-1 |
| 1 |
| t |
∴y≥3+
| 1 |
| 3 |
| 10 |
| 3 |
∴要使γ≤
| 3Snan+2 |
| 2Sn |
则γ≤
| 10 |
| 3 |
即γ∈(-∞,
| 10 |
| 3 |
故正确的是②③,
故答案为:②③.
点评:本题主要考查数列的递增公式的应用,考查学生的运算和推理能力.正确应用等比数列的通项公式和前n项和公式是解决本题的关键.

练习册系列答案
相关题目
由200名学生的某次数学考试成绩绘制成了频率分布直方图(如图).由图可知在该次数学考试中成绩小于60分的学生数是( )


| A、600 | B、60 | C、40 | D、4 |
已知⊙M经过双曲线S:
-
=1的一个顶点和一个焦点,圆心M在双曲线上S上,则圆心M到双曲线S的中心的距离为( )
| x2 |
| 9 |
| y2 |
| 16 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
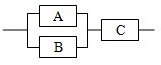 某个部件由三个元件如图方式连接而成,元件A或元件B正常工作,且元件C正常工作,则部件正常工作.若3个元件的次品率均为
某个部件由三个元件如图方式连接而成,元件A或元件B正常工作,且元件C正常工作,则部件正常工作.若3个元件的次品率均为