题目内容
已知a>1,b>1,且lnalnb=
,则ab( )
| 1 |
| 4 |
| A、有最大值1 |
| B、有最小值1 |
| C、有最大值e |
| D、有最小值e |
考点:基本不等式
专题:计算题,不等式的解法及应用
分析:根据题意,由基本不等式的性质可得lna+lnb≤(
)2,进而对其变形可得
≥
,结合对数的运算性质可得ab≥e;即可得答案.
| lna+lnb |
| 2 |
| lna+lnb |
| 2 |
| 1 |
| 2 |
解答:
解:根据题意,a>1,b>1,则lna>0,lnb>0;
由基本不等式可得:lna+lnb≤(
)2,
又由lnalnb=
,
即
≥
,
变形可得ab≥e;
即ab有最小值e;
故选:D.
由基本不等式可得:lna+lnb≤(
| lna+lnb |
| 2 |
又由lnalnb=
| 1 |
| 4 |
即
| lna+lnb |
| 2 |
| 1 |
| 2 |
变形可得ab≥e;
即ab有最小值e;
故选:D.
点评:本题考查基本不等式的应用以及对数的运算性质,注意基本不等式应用的3个条件.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
已知⊙M经过双曲线S:
-
=1的一个顶点和一个焦点,圆心M在双曲线上S上,则圆心M到双曲线S的中心的距离为( )
| x2 |
| 9 |
| y2 |
| 16 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列命题中正确的是( )
A、若
| ||||||||||||
B、向量
| ||||||||||||
| C、空间任意两个向量共面 | ||||||||||||
D、若
|
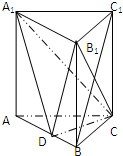 已知直三棱柱ABC-A1B1C1中,AC=BC,点D是AB的中点.
已知直三棱柱ABC-A1B1C1中,AC=BC,点D是AB的中点.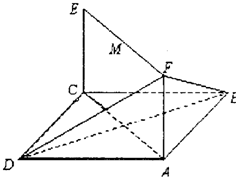 已知平行四边形ABCD和矩形ACEF所在的平面互相垂直,AB=1,AD=2,∠ADC=60°,AF=a(a>0)
已知平行四边形ABCD和矩形ACEF所在的平面互相垂直,AB=1,AD=2,∠ADC=60°,AF=a(a>0)