题目内容
1.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为120°,|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=5.(1)求$\overrightarrow{a}$•$\overrightarrow{b}$;
(2)求|3$\overrightarrow{a}$-$\overrightarrow{b}$|.
分析 (1)根据平面向量数量积的定义计算$\overrightarrow{a}$•$\overrightarrow{b}$;
(2)根据模长公式计算|3a-b|.
解答 解:(1)向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为120°,|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=5;
∴$\overrightarrow{a}$•$\overrightarrow{b}$=|$\overrightarrow{a}$|×|$\overrightarrow{b}$|cos120°=1×5×(-$\frac{1}{2}$)=-$\frac{5}{2}$;
(2)${(3\overrightarrow{a}-\overrightarrow{b})}^{2}$=9${\overrightarrow{a}}^{2}$-6$\overrightarrow{a}$•$\overrightarrow{b}$+${\overrightarrow{b}}^{2}$
=9×12-6×(-$\frac{5}{2}$)+52
=49,
∴|3a-b|=7.
点评 本题考查了平面向量的数量积与模长公式的应用问题,是基础题.

练习册系列答案
相关题目
11.已知a,b∈R,i是虚数单位,若a+i与2-bi互为共轭复数,则$\frac{b-i}{a+i}$=( )
| A. | $\frac{1}{5}$+$\frac{3}{5}$i | B. | $\frac{3}{5}$+$\frac{1}{5}$i | C. | $\frac{1}{5}$-$\frac{3}{5}$i | D. | $\frac{3}{5}$-$\frac{1}{5}$i |
12.已知{an}是公差为1的等差数列,Sn为{an}的前n项和,若S6=4S3,则a10=( )
| A. | $\frac{17}{2}$ | B. | $\frac{19}{2}$ | C. | $\frac{9}{10}$ | D. | $\frac{8}{9}$ |
9.下列命题正确的是( )
| A. | 若|$\overrightarrow{a}$|=|$\overrightarrow{b}$|,则$\overrightarrow{a}$=$\overrightarrow{b}$ | B. | 若|$\overrightarrow{a}$|>|$\overrightarrow{b}$|,则$\overrightarrow{a}$>$\overrightarrow{b}$ | C. | 若$\overrightarrow{a}$=$\overrightarrow{b}$,则$\overrightarrow{a}$∥$\overrightarrow{b}$ | D. | 若|$\overrightarrow{a}$|=0,则$\overrightarrow{a}$=0 |
6.球的半径扩大为原来的2倍,它的体积扩大为原来的( )倍.
| A. | 4 | B. | 8 | C. | 16 | D. | 64 |
10.若某个扇形的半径为3cm,弧长为πcm,则该扇形的面积为( )
| A. | πcm2 | B. | $\frac{3}{2}π$cm2 | C. | 3πcm2 | D. | 6πcm2 |
11.a、b均为实数,则a<b<0是a2>b2的( )
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
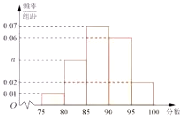 某地区有800名学员参加交通法规考试,考试成绩的频率分布直方图如图所示,其中成绩分组区间是:[75,80),[80,85),[85,90),[90,95),[95,100],规定90分及以上为合格:
某地区有800名学员参加交通法规考试,考试成绩的频率分布直方图如图所示,其中成绩分组区间是:[75,80),[80,85),[85,90),[90,95),[95,100],规定90分及以上为合格: