题目内容
在△ABC中,a,b,c分别为角A,B,C的对边,△ABC的面积为
,又tanA+tanB=-
(1-tanAtanB),则ab的值为 .
| ||
| 4 |
| 3 |
考点:正弦定理的应用,两角和与差的正切函数
专题:计算题,三角函数的求值,解三角形
分析:运用两角和的正切公式和内角和定理及诱导公式,得到tanC=
,再由三角形的面积公式,即可得到ab的值.
| 3 |
解答:
解:∵tanA+tanB=-
(1-tanAtanB),
∴tan(A+B)=
=-
,
∵A+B=π-C,∴tan(π-C)=-
,即tanC=
,
∵C=
,△ABC的面积为
,
∴
absinC=
absin
=
,即ab=1.
故答案为:1.
| 3 |
∴tan(A+B)=
| tanA+tanB |
| 1-tanAtanB |
| 3 |
∵A+B=π-C,∴tan(π-C)=-
| 3 |
| 3 |
∵C=
| π |
| 3 |
| ||
| 4 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 3 |
| ||
| 4 |
故答案为:1.
点评:本题考查三角形的面积的公式的运用,考查两角和的正切公式及运算能力,属于基础题.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
把复数z的共轭复数记作,i为虚数单位.若z=1+i,则(1+z)
等于( )
| z |
| A、3-i | B、3+i |
| C、1+3i | D、3 |
已知向量
=(2,1),
=(3,2),若
⊥(
+λ
),则实数λ等于( )
| a |
| b |
| a |
| a |
| b |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
若f(sin x)=3-cos 2x,则f(cos x)=( )
| A、3-cos 2x |
| B、3-sin 2x |
| C、3+cos 2x |
| D、3+sin 2x |
掷两枚均匀的骰子,已知第一枚骰子掷出6点,则两枚骰子“掷出的点数之和大于等于10”的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
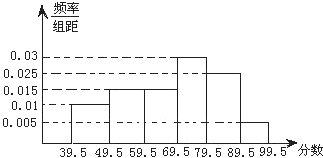 如图,从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如图:观察图形,回答下列问题:
如图,从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如图:观察图形,回答下列问题: