题目内容
5.已知直线l的参数方程为:$\left\{\begin{array}{l}{x=2t}\\{y=1+4t}\end{array}\right.$(t为参数),圆C的极坐标方程为$ρ=2\sqrt{2}sinθ$,则直线l与圆C的位置关系为( )| A. | 相切 | B. | 相交 | C. | 相离 | D. | 无法确定 |
分析 消去t为参数可得直线l的普通方程;根据x=ρcosθ,y=ρsinθ带入可得圆C的直角坐标方程.圆心到直线的距离与半径比较可得直角的关系.
解答 解:直线l的参数方程为:$\left\{\begin{array}{l}{x=2t}\\{y=1+4t}\end{array}\right.$,消去t为参数可得:2x-y+1=0.
圆C的极坐标方程为$ρ=2\sqrt{2}sinθ$,根据x=ρcosθ,y=ρsinθ带入可得:${x}^{2}+{y}^{2}=2\sqrt{2}y$,
圆心为(0,$\sqrt{2}$),半径r=$\sqrt{2}$.
那么:圆心到直线的距离d=$\frac{|-\sqrt{2}+1|}{\sqrt{5}}$
∵d$<\sqrt{2}$,
∴直线l与圆C相交.
故选B.
点评 本题主要考查了极坐标、参数方程与直角坐标方程的转换.点到直线的距离公式.属于基础题.

练习册系列答案
相关题目
15.如图是一个四棱锥的三视图,在所有侧面中直角三角形的个数有( )


| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
20.曲线的极坐标方程为ρ=2cosθ,则曲线的直角坐标方程为( )
| A. | (x-1)2+y2=1 | B. | x2+(y-1)2=1 | C. | (x-2)2+y2=1 | D. | x2+(y-2)2=1 |
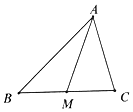 如图,锐角△ABC中,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,点M为BC的中点.
如图,锐角△ABC中,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,点M为BC的中点.