题目内容
13.函数f(x)=x2+2x,集合A={(x,y)|f(x)+f(y)≤2},B={(x,y)|f(x)≤f(y)},则由A∩B的元素构成的图形的面积是( )| A. | π | B. | 2π | C. | 3π | D. | 4π |
分析 根据已知中函数f(x)=x2+2x,集合A={(x,y)|f(x)+f(y)≤2},B={(x,y)|f(x)≤f(y)},画出满足条件的图形,进而可得答案.
解答 解:A={(x,y)|f(x)+f(y)≤2}={(x,y)|(x+1)2+(y+1)2≤4}
B={(x,y)|f(x)≤f(y)}={(x,y)|(x-y)(x+y+2)≤2}
画出可行域,正好拼成一个半径为2的半圆,
故S=$\frac{1}{2}$×22=2π
故选:B
点评 本题考查的知识点是集合的交集运算,简单线性规划的应用,数形结合思想,难度中档.

练习册系列答案
相关题目
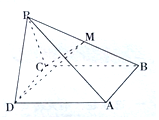 如图,在棱锥P-ABCD中,侧面PDC是边长为2的正三角形,底面ABCD是菱形,平面PCD⊥平面ABCD,M是PB的中点,且∠BCD=120°.
如图,在棱锥P-ABCD中,侧面PDC是边长为2的正三角形,底面ABCD是菱形,平面PCD⊥平面ABCD,M是PB的中点,且∠BCD=120°.